Philosophy

The fundamental features of the CMP program reflect the authors’ core beliefs about essential features of effective teaching and learning of mathematics. These features include a focus on big ideas and the connections among them, teaching through student-centered exploration of mathematically rich problems, and using continuous assessment to inform instruction.

• Overarching Goal of Connected Mathematics
• Guiding Principles
• A Problem Centered Curriculum
• Criteria for Mathematical Tasks
• Mathematical Fluency
• Depth vs Spiraling
• Instructional Model

Overarching Goal of Connected Mathematics

The overarching goal of CMP is to help students and teachers develop mathematical knowledge, understanding, and skill along with an awareness of and appreciation for the rich connections among mathematical strands and between mathematics and other disciplines. The CMP curriculum development has been guided by our single mathematical standard:

This goal has withstood the test of time through three research design and implementation cycles – design, develop, test, assess.

The CMP materials reflect the understanding that teaching and learning are not distinct— “what to teach” and “how to teach it” are inextricably linked. The circumstances in which students learn affect what is learned. The needs of both students and teachers are considered in the development of the CMP curriculum materials. This curriculum helps teachers and those who work to support teachers examine their expectations for students and analyze the extent to which classroom mathematics tasks and teaching practices align with their goals and expectations. In developing the CMP curriculum, the authors have taken the following words of Jerome Bruner to heart:

Guiding Principles 

The authors were guided by the following principles in the development of the CMP materials. These statements reflect both research and policy stances in mathematics education about what works to support students' learning of important mathematics.

• CMP is problem-centered. Mathematical tasks for students in class and in homework are the primary vehicle for student engagement with the mathematical concepts to be learned. The key mathematical goals are elaborated, exemplified, and connected through the Problems in an Investigation.
• CMP identifies big ideas and goes for depth. Ideas are explored through these mathematical tasks in the depth necessary to allow students to make sense of them. Superficial treatment of an idea produces shallow and short-lived understanding and does not support making connections among ideas.
• CMP has coherence. The underlying concepts, skills, or procedures supporting the development of a key idea are identified and included in an appropriate development sequence. The curriculum builds and connects from Problem to Problem, Investigation to Investigation, Unit to Unit and grade to grade.
• CMP intertwines conceptual and procedural knowledge. The curriculum helps students grow in their ability to reason effectively with information represented in graphic, numeric, symbolic, and verbal forms and to move flexibly among these representations to produce fluency in both conceptual and procedural knowledge.
• CMP develops skills and concepts as needed. Concepts and skills are developed, as appropriate, to solve interesting and challenging problems.
• CMP promotes inquiry-based instruction. Classroom instruction focuses on inquiry and investigation of mathematical ideas embedded in rich problem situations through rich classroom discourse and collaborations.
• CMP promotes effective use of technology. The curriculum reflects the information-processing and delivery capabilities of calculators and computers and the fundamental changes such tools are making in the way people learn mathematics and apply their knowledge of problem solving to new tasks.
• CMP has high expectations of all students. All students are asked sophisticated mathematical questions and are expected to persevere in their explorations to these questions, looking for patterns, generalizing, validating, and sharing and critiquing each others work.

Top

A Problem Centered Curriculum  

Rationale for a Problem-Centered Curriculum

Students' perceptions about a discipline come from the tasks or problems with which they are asked to engage. For example, if students in a geometry course are asked to memorize definitions, they think geometry is about memorizing definitions. If students spend a majority of their mathematics time practicing paper-and-pencil computations, they come to believe that mathematics is about calculating answers to arithmetic problems as quickly as possible. They may become faster at performing specific types of computations, but they may not be able to apply these skills to other situations or to recognize problems that call for these skills. Formal mathematics begins with undefined terms, axioms, and definitions and deduces important conclusions logically from those starting points. However, mathematics is produced and used in a much more complex combination of exploration, experience-based intuition, and reflection. If the purpose of studying mathematics is to be able to solve a variety of problems, then students need to spend significant portions of their mathematics time solving problems that require thinking, planning, reasoning, computing, and evaluating.

A growing body of evidence from the cognitive sciences supports the theory that students can make more sense of mathematics if the concepts and skills are embedded within a context or problem. If time is spent exploring interesting mathematics situations, reflecting on solution methods, examining why the methods work, comparing methods, and relating methods to those used in previous situations, then students are likely to build more robust understandings of mathematical concepts and related procedures. This method is quite different from the assumption that students learn by observing a teacher as he or she demonstrates how to solve a problem and then practicing that method on similar problems. A problem-centered curriculum not only helps students to make sense of the mathematics, but also helps them to process the mathematics in a retrievable way.

Teachers of CMP report that students in succeeding grades remember and refer to a concept, technique, or problem-solving strategy by the name of the Problem in which they encountered the ideas. For example, the Basketball Problem from What Do You Expect? in grade 7 becomes a trigger for remembering the processes of finding compound probabilities and expected values.

Results from the cognitive sciences also suggest that learning is enhanced if it is connected to prior knowledge and is more likely to be retained and applied to future learning. Critically examining, refining, and extending conjectures and strategies are also important aspects of becoming reflective learners.

In CMP, important mathematical ideas are embedded in the context of interesting problems. As students explore a series of connected problems, they develop an understanding of the embedded ideas and, with the aid of the teacher, abstract powerful mathematical ideas, problem-solving strategies, and ways of thinking. They learn mathematics and learn how to learn mathematics.

Top

Criteria for Mathematical Tasks  

To be effective, problems must embody critical concepts and skills and have the potential to engage students in making sense of mathematics. And, since students build understanding by reflecting, connecting, and communicating, the problems need to encourage them to use these processes.

Each CMP Problem has some or all of the following characteristics:

• Embeds important, useful mathematics
• Promotes conceptual and procedural knowledge
• Builds on and connects to other important mathematical ideas
• Requires higher-level thinking, reasoning, and problem solving
• Provides multiple access points for students
• Engages students and promotes classroom discourse
• Allows for various solution strategies
• Creates an opportunity for teacher to assess student learning

Top

Mathematical Fluency  

Students need to practice mathematical concepts, ideas, and procedures to reach a level of fluency that allows them to “think” with the ideas in new situations. To accomplish this, we were guided by the following principles related to skills practice.

• Immediate practice is related to the situations in which the ideas have been developed and learned.
• Continued practice uses reasoning, skills, and procedures in situations that connect to ideas that students have already encountered as well as to new situations.
• Practice is distributed over time to allow ideas, concepts and procedures to reach a level of fluency of use in familiar and unfamiliar situations and to allow connections to be made to other concepts and procedures.
• Students learn how to make judgments about what operation or combination of operations or representations is useful in a given situation, as well as become skillful in carrying out the needed computation(s); knowing how to, but not when to, is insufficient.

Top

Depth vs Spiraling  

  Example of Depth and Connectedness

The concept of a “spiraling” curriculum is philosophically appealing; but, too often, not enough time is spent initially with a new concept to build on it at the next stage of the spiral. This causes teachers to spend a great deal of time re-teaching the same ideas over and over again. Without a deeper understanding of concepts and how they are connected, students come to view mathematics as a collection of different techniques and algorithms to be memorized.

Problem solving based on such learning becomes a search for the correct algorithm rather than seeking to make sense of the situation, considering the nature and size of a solution, putting together a solution path that makes sense, and examining the solution in light of the original question. Taking time for the ideas studied to be more carefully developed means that when these ideas are met in the future, students have a solid foundation on which to build. Rather than being caught in a cycle of relearning the same ideas at a superficial level, which are quickly forgotten, students are able to connect new ideas to previously learned knowledge and make substantive advances in learning.

With any important mathematical concept, there are many related ideas, procedures, and skills. At each grade level, a small, select set of important mathematical concepts, ideas, and related procedures are studied in depth rather than skimming through a larger set of ideas in a shallow manner. This means that time is allocated to develop an understanding of key ideas in contrast to “covering” a book. The teacher support materials accompanying CMP were developed to support teachers to plan for and teach a problem-centered curriculum. Practice on related skills and algorithms is provided in a distributed fashion so that students not only practice these skills and algorithms to reach facility in carrying out computations, but they also learn to put their growing body of skills together to solve new problems.

Top

Instructional Model  

An Inquiry-Based Classroom

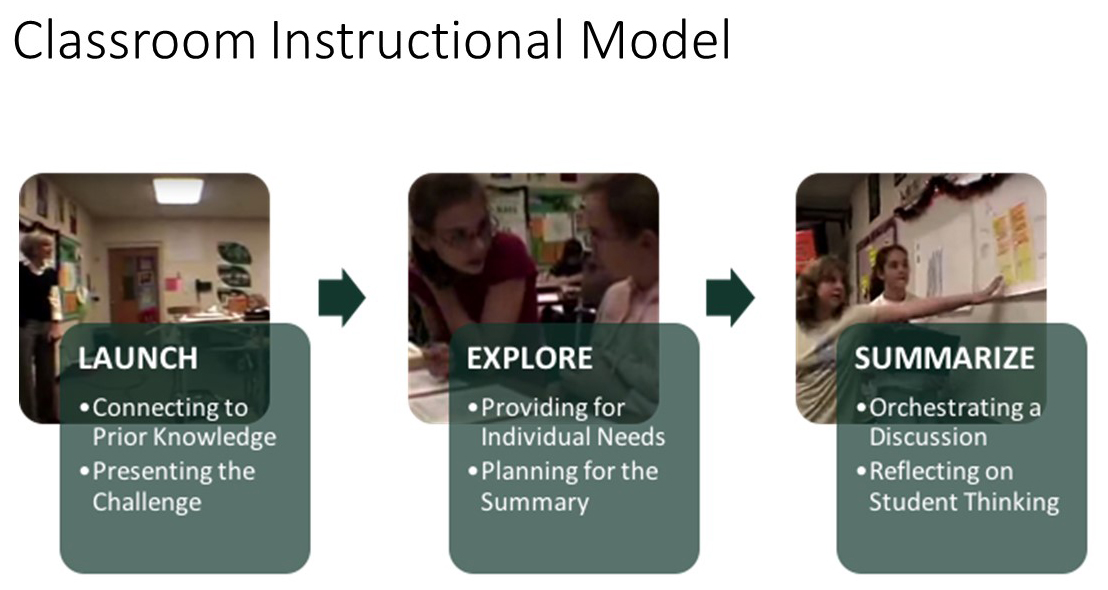
Problem-centered teaching and learning opens the mathematics classroom to exploring, conjecturing, reasoning, and communicating. Both the teacher and student take on more responsibility for the learning process. The CMP teacher materials are organized around an instructional model that supports this kind of “inquiry-based” teaching. This model is very different from the “transmission” or “direct instruction” model, in which teachers tell students facts and demonstrate procedures and then students memorize the facts and practice the procedures. The CMP model looks at instruction in three phases: launching, exploring, and summarizing.

Teacher Roles

When mathematical ideas are embedded in problem-based investigations with rich context, the teacher takes on more responsibility for student learning. The teacher must ensure that students abstract and generalize the important mathematical concepts and procedures from their experiences with the problems. The teacher guides, prompts, questions, and facilitates the learner to do and make sense of the mathematics. In a problem-centered classroom, teachers move from demonstrating how to do the mathematics to one who guides, prompts, questions, and facilitates the learner to do and make sense of the mathematics. In these new roles, teachers grow their ability to recognize and use student thinking more effectively in developing a deeper understanding, reasoning, and skills. Witnessing students collaborating, challenging each other, thinking in new ways, gaining mathematical confidence, and communicating these ideas is worth the effort. Extensive mathematical and pedagogical help is provided in the teacher guide for each unit. General support for teachers and information on the teacher role can be found in the Guide to Connected Mathematics 3 and in the following places on the website.

• Teacher Materials
• Classroom
• Teacher Support
• CMP Classroom Observation Guide
• Classroom Instructional Model
  • Launch
  • Explore
  • Summarize

Student Roles

In a problem-centered classroom as the teacher’s role shifts, students take more responsibility for their learning by solving problems and then sharing and discussing their strategies and new mathematical understandings with the class. As a result, students develop deep understanding of mathematical concepts, skills, procedures, and processes. Under the guidance of the teacher, students take on the following roles during the instruction.

During the Launch, students make sense of the context and the challenge presented by the problem.

In the Explore, students continue to make sense of the challenge as they work with their classmates in small groups, pairs, or individually to:

• Observe patterns and relationships in a situation;
• Recognize and employ prior understandings to conjecture, test, discuss, verbalize, and generalize patterns;
• Justify their reasoning, including the expectation to make sense of the reasoning of their classmates;
• Discover salient mathematical features of patterns and relationships and abstract the underlying mathematical concepts, processes, and relationships; and,
• Make judgments about what operation, a combination of operations, or representation(s) is useful in a situation, as well as, become skillful at carrying out the needed computation(s).

During the Summarize the teacher and students work together to:

• Clarify their understanding and strategies by sharing it with others and critiquing the work of other students;
• Make visible the mathematics embedded in the problem;
• Develop a mathematical language for representing and communicating ideas; and
• Make sense of and connect mathematics abstracted from their experiences to prior learnings.

At the end of an Investigation, the students have a chance to reflect on the essential understandings and strategies of the Investigation in the Mathematical Reflections. At the end of the unit, students distill their learnings into one reflection in the Looking Back.

The CMP philosophy reflects the research on best practices that helps students develop meaningful and deep mathematical understanding. For example, “even though CMP was developed long before the publication of the National Academy of Science, Adding It Up (NRC, 2001)[1], the stances in this National Research Council publication’s five interrelated strands that comprise student proficiency are reflected in CMP. The first four NRC strands are conceptual understanding, procedural fluency, strategic competence (the ability to formulate, represent, and solve mathematical problems), and adaptive reasoning (the capacity to think logically and to informally and formally justify one’s reasoning). The fifth strand, productive disposition, is “the tendency to see sense in mathematics, to perceive it as both useful and worthwhile, to believe that steady effort in learning mathematics pays off, and to see oneself as an effective learner and doer of mathematics”(Lappan & Phillips 2008)[2]. More recently, the Common Core State Standards for Mathematical Practices (CCSSM 2009)³ reflect the strategies for engaging CMP students in productive mathematical learning.

Top