A unique feature of the CMP curriculum is that curriculum-generated student work is a context for student learning of mathematics. This project focuses on the role of student work found in curriculum materials and its potential for improving the teaching and learning of mathematics (Edson et al., 2017; Gilbertson et al., 2016; Gilbertson et al., 2016). In CMP4, the use of student work found in the Student Editions and teacher support help to (1) enhance student and teacher conceptual understanding and procedural fluency; (2) develop student agency, identity, authority, and ownership of mathematics; and (3) broaden student and teacher capacity to make sense of situations.

Over the years our knowledge of how and what students understand and the role of the teacher in this process has grown exponentially, Over the years the problems have taken on the burden of sharing this knowledge. For CMP4 we had the chance to deeply reflect on what is the challenge being presented; what is the embedded mathematics in the challenge; and how is this new knowledge connected to prior and future knowledge. Thus the STEM problem format consists of three phases: Initial Challenge, What If . . . ? and Now

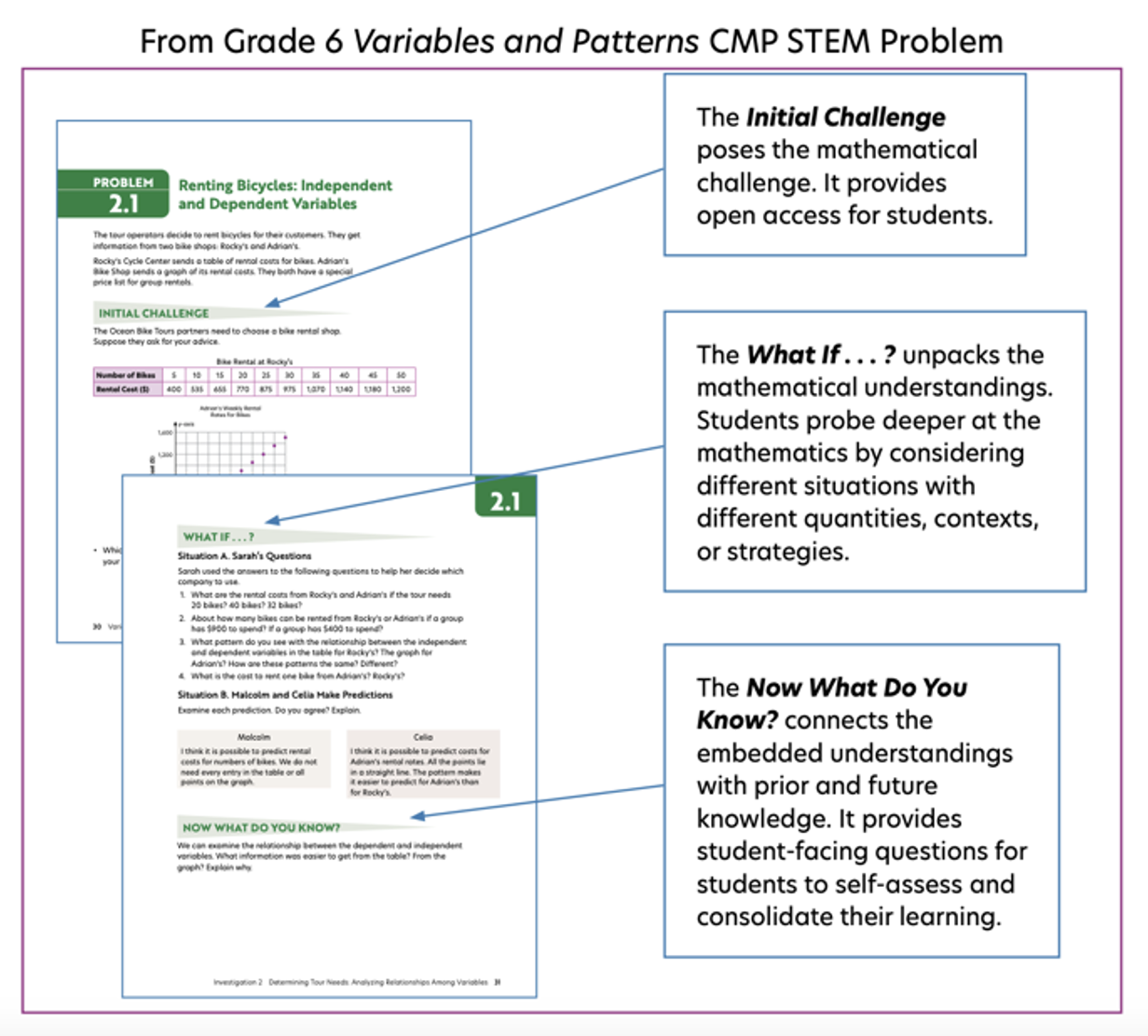
The Arc of Learning^TM Framework is a resource for curriculum design and use that makes explicit the intentions of the curriculum designers about how students engage in the learning of mathematics over time (Edson et al., 2016, 2017a, 2017b, 2019; Edson et al., 2019; Edson et al., 2015).

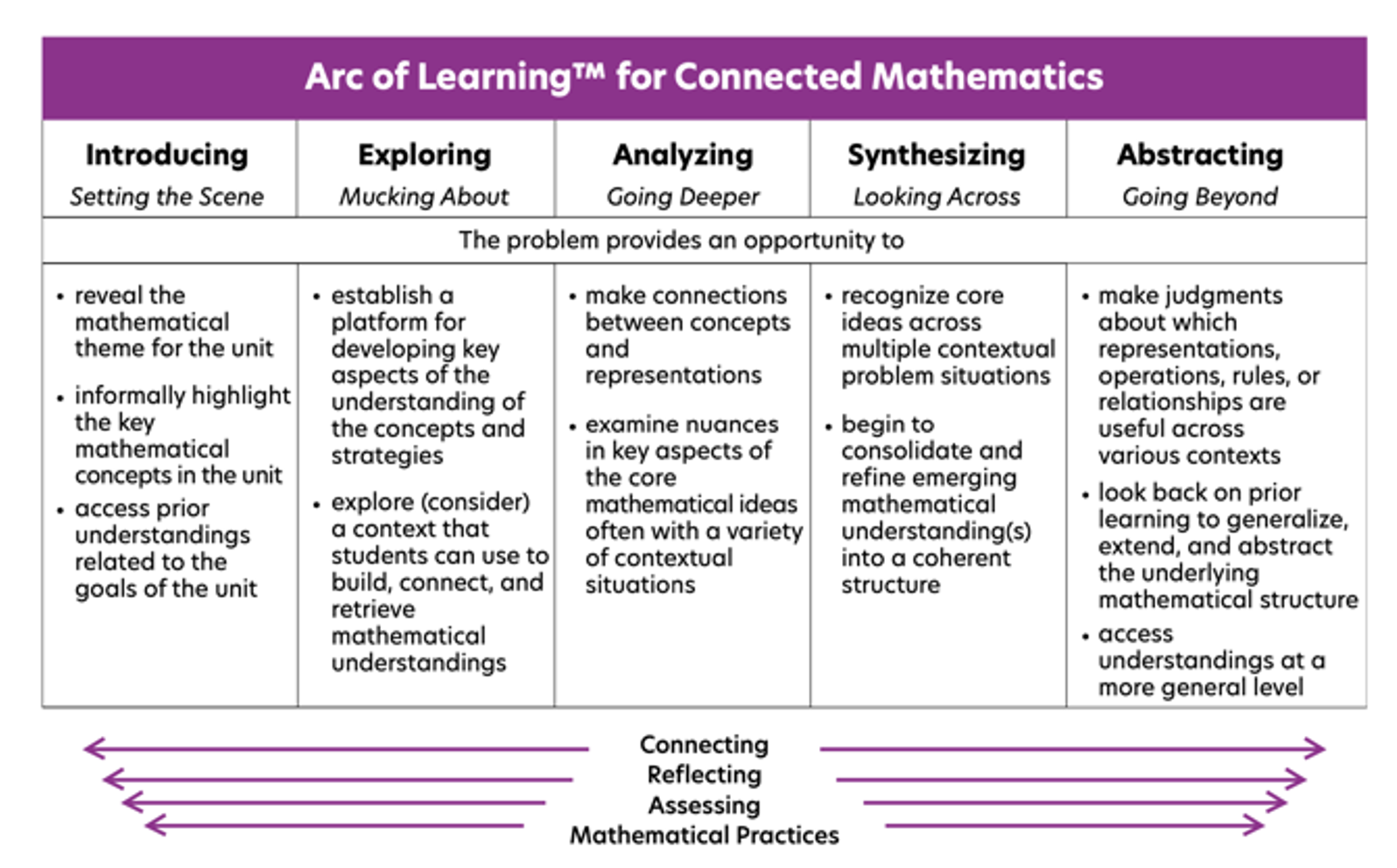
In CMP4, the Arc of Learning^TM framework informs

• how student thinking and learning is targeted and how that thinking and learning might unfold within and across mathematics sequences of problems;
• how teachers understand the development of long-term mathematical goals embedded in a coherent sequence of problems;
• the mathematical, pedagogical, and assessment decisions teachers make when planning or enacting lessons that respond to students’ mathematical conceptions;
• professional development to support problem-based learning; and the research and design on problem-based, contextualized curriculum.

As learners need different supports at different times in their learning, teachers attend to these diverse learning needs throughout classroom instruction. In CMP4, the Attending to Individual Learning Needs Framework provides teachers with ways to support diverse learning needs in rich mathematics problem-solving environments (Edson & Slanger-Grant, 2024, 2021; Edson et al., 2023). The differentiation framework highlights dimensions needed to enhance how students can access and engage with deep mathematical learning. The framework supports teachers in developing students as knowers and doers of mathematics by focusing on students’ strengths, backgrounds, and experiences. The five components of the framework include

• establishing a problem-solving environment that advances the mathematical understandings for each student;
• developing student agency, identity, and ownership of the mathematics;
• enhancing the portrayal of the mathematical ideas;
• bridging language to connect with students’ mathematical understandings; and
• allowing sufficient time to learn mathematical ideas through a sequenced set of tasks.

The teacher support materials give teachers guidance on using the Attending to Individual needs components.

Teachers assess student learning of mathematics throughout a CMP lesson. This project focuses on developing a set of resources to help mathematics teachers and instructional leaders make sense of formative assessment as an ongoing process in CMP classrooms. (Ray et al., 2017; Ray et al., 2016; Ray et al., 2016; Ray et al., 2015). This project was funded by CMP royalties from the MSU authors and administration to support research and development in mathematics education.

In this project, we report on field-testing and professional learning experiences of the fourth edition of the Connected Mathematics curriculum involving over 500 teachers from the United States and six countries. We ground our study in the theoretical and empirical curriculum design and enactment tensions that emerge in problem-based mathematics classrooms. We report on field-testing and professional learning experiences of the fourth edition of the curriculum involving over 500 teachers from the United States and six countries. This includes data analysis and feedback from four years of field-testing that reflect the interactions between teachers and students with the materials, including unit and problem feedback, teacher support, and assessment feedback to highlight changes made in curriculum design. Finally, we discuss implications for how the curriculum design and development process helps provide cohesive and effectively sequenced materials to support students and teachers in rich mathematical problem-solving experiences. (2025 paper in progress.)

This project is designing course materials for preservice teachers (PST) using some part of Connected Mathematics4. The materials provide four modules, each of which consists of four or five lessons. Each lesson contains two-part activities: (Part 1) PSTs experience student and teacher roles in solving mathematics problems embedded within real-world contexts), and (Part 2) PSTs reflect on teacher roles in such student-centered learning environments to connect with research-based teaching practices, theories, and pedagogy in mathematics education literature. The Part 1 activity utilizes one CMP curriculum unit (Moving Straight Ahead) that includes both the Student Edition and the Teacher Guide. Materials for each lesson include learning goals for PSTs, lesson outlines, suggested reading assignments, suggested discussion questions, additional readings/resources, and handouts. The modules aim to support PSTs in developing a deeper understanding of teaching and learning mathematics in a problem-based, inquiry-oriented classroom. Each of the four modules has both mathematical and pedagogical themes. (2024-in progress).

The royalties that MSU receives from the sales of its existing editions of CMP are used to fund research and development in mathematics and science education, including continual evaluation and revision of the CMP curriculum. These funds are also used to build capacity for mathematics educators and educational researchers. This includes several Lappan- Phillips Endowed Professorships and a Lappan-Phillips-Fitzgerald Endowed Mathematics Education Chair at Michigan State University. So far, over 70 graduate students have received assistantships, with many of them completing their dissertations in CMP classrooms; the funds have also supported science educators and postdoctoral researchers. These funds also provide professional development and leadership opportunities for teachers and district leaders. Out of the 20,000 participants at CMP events, more than 300 CMP ambassadors have served as workshop leaders, conference presenters, and mathematical coaches under the mentorship of the CMP author team.

A unique feature of the CMP curriculum is that curriculum-generated student work is a context for student learning of mathematics. This project focuses on the role of student work found in curriculum materials and its potential for improving the teaching and learning of mathematics.

In collaboration with the Concord Consortium, the project has designed a student and teacher digital collaborative platform for face-to-face instruction where each student has one-to-one access to laptops connected to the internet (Edson, 2024; Edson & Phillips, 2021, 2022; Edson et al., 2018, 2019; Edson et al., 2018; Going et al, 2018). The teacher typically has a computer in their classroom that is connected to a projection system, as well as a tablet that they can use to access the teacher digital dashboard and classroom workspace. The CMP STEM problem format emerged in part during this research project as the development team considered new ways to (re)design mathematics problems in a digital environment. This project is funded by several large research grants awarded by the National Science Foundation.

• Promoting Productive Disciplinary Engagement and Learning with Open Problems and "Just-in-Time" Supports in Middle School Mathematics (NSF Core Grant) 2017-2022
• Collaborative Research: Enhancing Middle Grades Students' Capacity to Develop and Communicate Their Mathematical Understanding of Big Ideas Using Digital Inscriptional Resources (NSF DRK12 Grant) 2016-2022 
• Enhancing the Teacher-Curriculum Relationship in Problem-Based Mathematics Classrooms by Connecting Teacher and Student Digital Collaborative Environments (NSF DRK12 Grant 2020-2024)
• Using Problem-Based Learning Analytics to Investigate Individual and Collaborative Mathematics Learning in a Digital Environment Over Time(NSF DRK12 Grant 2022-2026)
• Promoting Student Engagement and Learning in Proportional Reasoning Over Time
  Using Artificial Intelligence Based on Evidence of Student Thinking (NSF DRK12) Submitted November 2024