Frequently Asked Questions

Your student’s book and notebook is a place to find the mathematics studied each day. Your student will work with their teacher to record important mathematical ideas, key terms, and procedures.

 

Every lesson in CMP is structured around a STEM Problem Format.

• A problem is posed in an Initial Challenge to provide open access to the mathematics. Students will engage with an important mathematical idea embedded in a context.
  
  
• In the What If…?,students will unpack mathematical ideas. They probe deeper by considering different situations with different quantities, context, skills, or strategies. Students will exam various quantities, scenarios, and strategies to deepen and connect mathematical concepts.
  
  
• A Now What Do You Know? Question has students describing their learning from the lesson. Students will connect new mathematical insights with both past and current knowledge.

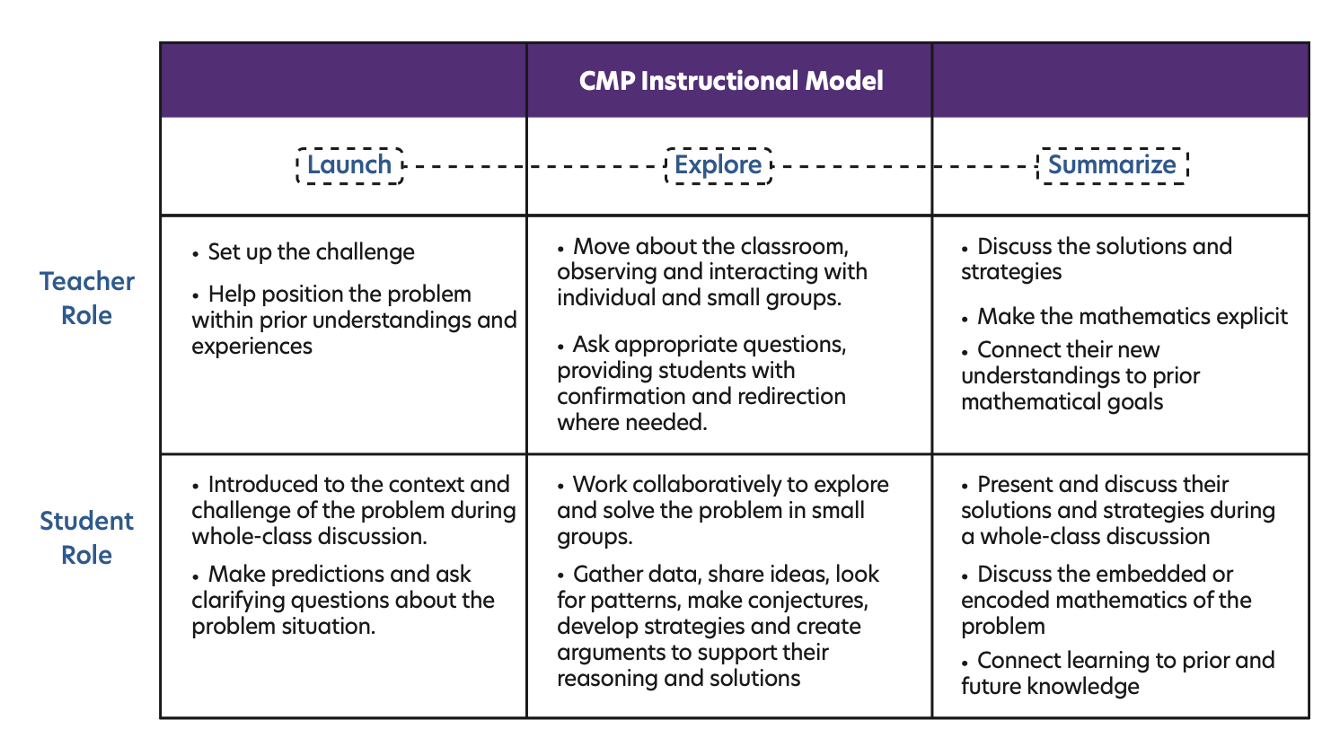
CMP lessons are designed around a Launch-Explore-Summarize pattern.

• In a typical lesson, the teacher starts by launching the problem. Teachers help students connect to prior learning and work through important terms or aspects of the problem(s).
  
  
• Then, students explore the mathematical ideas by working on problems individually or with other students. Depending on the purpose of the problem, the explore phase might look a little different. It might involve students just suggesting ideas for discussion. Or, it might involve students analyzing big ideas and putting multiple ideas together to construct core understandings. Teachers monitor students, attend to individual needs, and ask probing questions to enhance students learning from the problems.
  
  
• Finally, the teacher leads a summary discussion. Using students’ thinking and strategies, the class summarizes the important mathematical ideas and skills for the lesson.

CMP was designed to be compatible with cognitive science research about how people learn. Specifically, it supports communication about mathematics between students and between students and the teacher. The single mathematical standard that has been a guide for all the CMP curriculum development is that all students should be able to reason and communicate proficiently in mathematics.

If students are to reason and communicate proficiently, then student must spend time practicing these skills in the classroom. Sometimes students work individually and write explanations of their thinking, but often students discuss problems, argue with and convince each other, make conjectures and draw conclusions, and make summaries—things that mathematicians do! The teacher's role is to guide students as they work with problems to develop understanding of the embedded ideas, and explore powerful mathematical principles, strategies and algorithms.

Of course, there are occasions when the teacher demonstrates mathematical ideas, but generally the teacher will try to help students draw as much sense as they can from a problem before intervening.

In the Homework Support pages, we offer suggestions for how you can help your student. At home, you can encourage your students’ independence as a mathematics by asking thoughtful questions during homework time. Instead of giving the answer, guide them to explain their reasoning step by step. This helps your student take ownership of their learning and become a more confident problem solver.

CMP4 is a contextual problem-based curriculum which is a departure from the traditional classroom in which most of us have learned or taught. The Investigations and Problems encourage students to explore, conjecture, validate, and communicate their ideas.

Contextualized problems provide students with opportunities to make sense of the world and empower them to use mathematics to solve problems. The context of the problem helps students develop important mathematical understanding and skills. It also helps them retrieve and apply their knowledge as needed for future learning.

The contexts provide opportunities for students to elicit genuine interest and wonderment in the context itself, access to the mathematics problem, anchor instruction in a context to develop understanding, and highlight applications of mathematics in everyday matters. 

The problems also provide students with opportunities to affirm, value, and build on their experiences through their families’ and communities’ cultural and linguistic funds of knowledge. This mathematical and pedagogical grounding is valuable for all students and it helps students reach their full potential.

You can still have meaningful mathematical conversation with your student.

• Your child may have a mathematics notebook with a record of class ideas, strategies, examples, solutions, and vocabulary.
  
  
• Without being part of the classroom discussion, it can be hard to reconstruct the mathematics embedded in the problems. To help you bridge this gap, there are Family Letters for each unit. It includes concepts, important vocabulary, mathematical goals, and examples to help families support their student along the way.
  
  
• In the Homework Support pages, we offer suggestions for how you can help your student.
  
  
• You might find the Glossary We have mathematical terms with examples that students will explore during the 6^th, 7^th, and 8^thgrades.

The overarching goal in CMP is for students to make sense of and take ownership of mathematical concepts. Students learn effectively when they take on the role of formulating, representing, clarifying, communicating, and reflecting on ideas.

Examples are done by students during class as they work independently, in groups, or with the help of the teacher. Their work is captured in their notebooks or other recording resources, so students can refer to it whenever needed.

Your student should be keeping notes about how they solve problems in class. This includes writing down new vocabulary, summarizing each problem (with support from the teacher), completing the Now What Do You Know? section for each problem, and the Mathematical Reflection at the end of each investigation. While teachers may organize notebooks differently, the goal is the same: to create a clear record of what your student understands and can do. These notebooks are essential to your student’s success and can be a helpful resource when they’re working on math at home.

You might find the Getting Organized suggestions in the Homework Support helpful.

CMP4 introduces algebra in the first unit of Grade 6, Variables and Patterns. Then over the three years of CMP4, students continue to experience a coherent functions approach to learning about important mathematical relationships, including linear, exponential, quadratic, and inverse variation relationships. They also learn how to solve linear, exponential, and quadratic equations. CMP4’s unique approach to combine conceptual and procedural knowledge, and its unique development of algebra and functions into one strand provides a solid Algebra 1 foundation in Grade 8. There are two paths through Grade 8: Grade 8 and Algebra I.

CMP4 algebra units are an excellent preparation for a functions-based approach in Algebra 2. Because of this extensive and thorough study of algebraic ideas in CMP4, a student who continues their mathematics path in high school will be prepared to take college-level courses, including calculus, by the end of their senior year of high school.

Of the 23 total units spanning the three grade levels, eight are dedicated to developing geometry and measurement concepts. The CMP4 authors were influenced by mathematics education research indicating a shift from a focus on shape and form to the related ideas of congruence, similarity, and symmetry transformations.

High school Geometry courses typically spend a semester on shape and measurement and a semester on proving. Shape and measurement are two topics thoroughly explored in CMP. All CMP units require students to reason and communicate their reasoning, which means they have a strong foundation for writing proofs. In CMP geometry units, students are asked to reason about ideas that are part of the high school curriculum, such as similarity and congruence. At first the reasoning will be informal, but their ability to reason and their ability to communicate their reasoning continues to develop over each unit and year.

Students draw upon the contexts of the problems to help them recall the mathematics associated with those contexts. In addition, these real-life situations and the STEM problem format provide a transition into the world of symbols, helping students to make sense of the symbols even in abstract situations. Solving such problems requires using many kinds of mathematical skills, so students are constantly practicing important skills as well as developing understanding and advancing their reasoning.

 

Introducing a mathematical idea through a contextual problem that embodies the concept invites students into thinking mathematically and promotes students as problem solvers. It allows students to develop meaning and use their knowledge to solve the problem.

CMP4 helps students reach their full potential. CMP4 is a coherent set of materials designed to guide teachers and students in the development of mathematical knowledge that includes deep understanding, proficiency in skills, and the ability to make connections within mathematics and connections to other disciplines. In CMP, this is accomplished by embedding the mathematics in problem situations.

 

In short, CMP values both skills and concepts, and the authors have created ways for students to develop concepts and practice skills, and for teachers to assess both.

In Research on CMP, you can find studies comparing CMP students and their peers in more traditional curricula. Many of these studies indicate that their performance is similar on tests of basic skills, and CMP students perform significantly better on assessments of conceptual understanding and problem solving.

Effective strategies for diverse populations of students are already built into the CMP curriculum. These design features of the student materials include:

• Units built around big ideas
• Development of ideas around the Arc of Learning™ Framework
• Lesson presented through the STEM Problem Format
• Overarching Mathematical Reflections over the course of a unit
• Did You Know? enhancement informational boxes
• Lessons designed around the Launch—Explore—Summarize instructional model

 

The teacher materials include extensive support for teachers as they implement CMP. For each problem in the CMP4 Teacher Edition, teachers are provided support for academically gifted students. This includes a framework for Attending to Individual Learning Needs. The framework helps to provide a curriculum appropriate for academically gifted students. The framework supports teachers in developing students as knowers and doers of mathematics by focusing on students’ strengths, backgrounds, and experiences. As learners need different supports at different times in their learning, teachers attend to these diverse learning needs throughout classroom instruction.

 

Evidence suggests that CMP can be and has been successfully implemented in classrooms that include students with special needs, academically gifted students, historically and culturally underrepresented students, and multilingual students. 

One of the important guiding principles of CMP is that the curriculum maintains high expectations of all students. All students should have access to appropriate levels of challenge and support. Effective strategies for diverse populations of students are already built into the CMP curriculum. These design features of the student materials include:

• Units built around big ideas
• Development of ideas around the Arc of Learning™ Framework
• Lesson presented through the STEM Problem Format
• Overarching Mathematical Reflections over the course of a unit
• Did You Know? enhancement informational boxes
• Lessons designed around the Launch—Explore—Summarize instructional model

 

The problems also provide students with opportunities to affirm, value, and build on their experiences through their families’ and communities’ cultural and linguistic funds of knowledge. This mathematical and pedagogical grounding is valuable for all students.

 

Several strategies are outlined and illustrated for each lesson to support teachers as they meet the unique needs of students who are learning English. The teacher materials include extensive support for teachers as they implement CMP. This includes a framework for Attending to Individual Learning Needs. The framework supports teachers in developing students as knowers and doers of mathematics by focusing on students’ strengths, backgrounds, and experiences. As learners need different supports at different times in their learning, teachers attend to these diverse learning needs throughout classroom instruction. The Teacher Editions provides support for teachers using the AILN components are in every lesson.

 

It’s important to note that none of these strategies involves modifying the cognitive demand of the mathematics in CMP. That is, every effort has been made to support all students in gaining a rich understanding of important mathematics.

 

Evidence suggests that CMP can be and has been successfully implemented in classrooms that include students with special needs, academically gifted students, historically and culturally underrepresented students, and multilingual students. 

Effective strategies for diverse populations of students are already built into the CMP curriculum. These design features of the student materials include:

• Units built around big ideas
• Development of ideas around the Arc of Learning™ Framework
• Lesson presented through the STEM Problem Format
• Overarching Mathematical Reflections over the course of a unit
• Did You Know? enhancement informational boxes
• Lessons designed around the Launch—Explore—Summarize instructional model

 

One of the important guiding principles of CMP is that the curriculum maintains high expectations of all students. All students should have access to appropriate levels of challenge and support. The Teacher Edition for each lesson pays detailed attention to students with special needs in the mathematics classroom. These strategies are discussed in the CMP4 Attending To Individual Needs Framework (AILN). The Teacher Editions provides support for teachers using the AILN components are in every lesson. 

The important thing to know is that none of these strategies involves modifying the cognitive demand of the mathematics in CMP. That is, every effort has been made to support all students in gaining a rich understanding of important mathematics.

Supports for students with special needs are often strategies that help all children learn. Blending group and individual work, student conversation and silent reflection, and conceptual development and procedural skills practice--characteristics that are integral to CMP's format—offer more ways for students with a diverse range of skills to be successful.

 

Evidence suggests that CMP can be and has been successfully implemented in classrooms that include students with special needs, academically gifted students, historically and culturally underrepresented students, and multilingual students.

The problems in the Connected Mathematics4 program resemble the

work that STEM professionals do to solve problems, build deep knowledge and skills, and meaningfully connect the solutions to inform the needs of society. The STEM problem format promotes student engagement and learning as students collaborate to design solutions, make conjectures, offer critiques, and communicate their mathematical understandings.

Each lesson in CMP is structured around a STEM Problem Format.

• The Initial Challenge poses the mathematical challenge.  It provides open access for students. Students will engage with an important mathematical idea embedded in a context. The context may be real world, mathematical, connected to the real world, whimsical, abstract, mathematical, or imaginary.
  
  
• In the What If…?,students will unpack mathematical understandings. They probe deeper by considering different situations with different quantities, context, strategies, or skills which deepens their understanding of the embedded mathematics and connects it prior mathematical concepts.
  
  
• A Now What Do You Know? question asks students to describe their learning from the lesson. Students will connect new mathematical insights with both past and current knowledge. It provides student-facing questions for students to self-assess and consolidate their learning.

At the end of the set of problems in an Investigation, students reflect on what they have learned in the Mathematical Reflections. Students encounter the same unifying question after each investigation of the unit. 

The question is designed to help students incrementally organize their thoughts throughout a unit and summarize important concepts and strategies.

Students can use their findings from the Now What Do You Know? questions in each problem to begin to consolidate their understandings in the Mathematical Reflection. After thinking about the question and sketching their own ideas, students discuss the questions with their teacher and their classmates and then write a summary of their findings.

The goal of this activity is to have students reflect, consolidate, and assess their learning.

These are opportunities for students to Apply, Connect and Extend their understanding.

They are meant to be used as additional practice to apply, connect, and extend students’ mathematical concepts and skills. Students are asked to compare, visualize, model, measure, count, reason, connect, and/or communicate their ideas. To truly own an idea, strategy, or concept, a student must apply it, connect it to what they already know or have experienced, and seek ways to extend or generalize it.

 

Applications practice the ideas and strategies using contexts similar to and different from the those in the investigation. 

Connections offer continued review of concepts and skills across the grades.

Extensions provide new challenges for students to think beyond what is covered in class.

Each unit has at least one partner quiz. Quiz questions are richer and more

challenging than checkup questions. Many quiz questions are extensions of ideas students explored in class. These questions provide insight into how students apply the ideas from the unit to new situations. The partner quiz is an assessment that is meant to mirror and value the working environment in the classroom.

 

These are more complex than Checkup assessments and more closely resemble the work the students do during class, which prepares them for the work done by STEM professionals.

 

While individual teachers may adapt the quiz to fit the needs of their classes, the quizzes were created with the following assumptions:

• Students work in pairs.
• Students are permitted to use their notebooks and any other appropriate materials, such as calculators.
• Pairs have an opportunity to submit a draft of the quiz for teacher input. They may then revise their work and turn in the finished product.