6-1 Prime Time - Concepts and Explanations
Order of Operations
The universally agreed upon order for solving math problems. The acronym PEMDAS is used to help remember the order of the steps.
Example
- Compute any expression with parentheses.
- Compute any exponent.
- Do all multiplication and division in order from left to right.
- Do all addition and subtraction in order from left to right.
(4 + 6) x 2 = (10) x 2
= 20
Distributive Property
The Distributive Property shows how a number can be written as two equivalent expressions. A number can be expressed as both a product and a sum. Multiplication is distributed over addition. It can be helpful for understanding the structure of multidigit multiplication.
Example
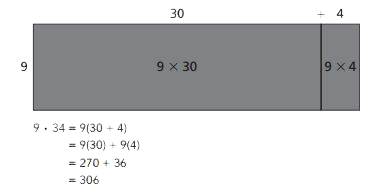
Prime
A number with exactly two factors, 1 and the number itself.
Example
Examples of primes are 11, 17, 53, and 101. The number 1 is not a prime number, since it has only one factor.
All of the factors of 11 are 1 and 11. All of the factors of 17 are 1 and 17.
Composite
A whole number with factors other than itself and 1 or a whole number that is not prime.
Example
Some composite numbers are 6, 12, 20, and 1,001. Each of these numbers has more than two factors.
All of the factors of 6 are 1, 2, 3, 6. All of the factors of 1,001 are 1, 7, 11, 13, 77, 91, 142 and 1001.
Common Multiples
A multiple that two or more numbers share. The least common multiple (LCM) of 12 and 18 is 36.
Example
The first few multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, and 70.
The first few multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, and 91.
From these lists you can see that two common multiples of 5 and 7 are 35 and 70. There are more common multiples that can be found.
Common Factors
A factor that two or more numbers share. The greatest common factor (CGF) of 12 and 18 is 6.
Example
The number 7 is a common factor of 14 and 35 because 7 is a factor of 14 (14 = 7 x 2) and 7 is a factor of 35 (35 = 7 x 5).
Prime Factorization
A product of prime numbers, resulting in the desired number. The prime factorization of a number is unique except for the order of the factors. This is the Fundamental Theorem of Arithmetic.
Example
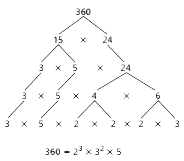
The prime factorization of 360 is 2 x 2 x2 x3 x5.
Although you can switch the order of the factors, every prime product string for 360 will have three 2s, two 3s and one 5.