7-3 Stretching and Shrinking - Concepts and Explanations
Corresponding
Corresponding sides or angles have the same relative position in similar figures.
Example
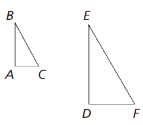
Corresponding Sides
- AC and DF
- AB and DE
- BC and EF
Corresponding angles
- A and D
- B and E
- C and F
Similarity
Two figures are similar if: (1) the measures of their corresponding angles are equal and (2) the lengths of their corresponding sides increase by the same factor, called the scale factor.
Example
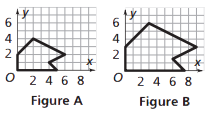
The two figures at the right are similar.
The corresponding angle measures are equal.
The corresponding side lengths in Figure B are 1.5 times as long as those in Figure A.
So, the scale factor from Figure A to Figure B is 1.5. (Figure A stretches or is enlarged by a factor of 1.5, resulting in Figure B.)
We also say that the scale factor from Figure B to Figure A is 1/1.5 or 2/3. (Figure B shrinks by a factor of 2/3, resulting in figure A).
Scale Factor
The number used to multiply the lengths of a figure to stretch or shrink it into a similar image.
A scale factor larger than 1 will enlarge a figure. A scale factor between 0 and 1 will reduce a figure.
The scale factor of two similar figures is given by a ratio that compares the corresponding
sides:
length of a side on the image/ length of a side on the original.
Example
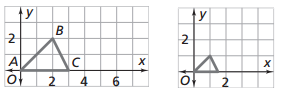If we use a scale factor of 1/2, all lengths in the images are 1/2 as long as the corresponding lengths in the original.
The base of the original triangle is 3 units.
The base of the image is 1.5 units.
The scale factor is 1.5/3 = 3/6 = 1/2.
Area and Scale Factor
Lengths of similar figures will stretch (or shrink) by a scale factor. Areas of the figures will not change in the same way.
Example
Applying a scale factor of 2 to a figure increases the area by a factor of 4.
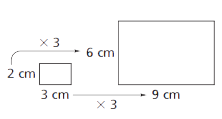
Applying a scale factor of 3 to a figure, increases the area by a factor of 9. The
original area is 6 cm2. The area of the image is 9 times as large (54 cm2).