8-3 Growing, Growing, Growing - Concepts and Explanations
Exponential Growth
An exponential pattern of change can often be recognized in a verbal description of a situation or in the pattern of change in a table of (x, y) values.
The exponential growth in rewards for good-work days in the example can be represented in a graph. The increasing rate of growth is reflected in the upward curve of the plotted points.
Example
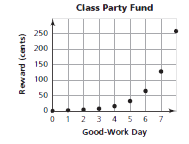
Suppose a reward is offered for days of good work. At the start, 1¢ is put in a party fund. On the first good-work day, 2. is added; on the second good-work day, 4. is added; and on each succeeding good-work day, the reward is doubled. How much money is added on the eighth good-work day?
| Good-Work Day | Reward (cents) |
|---|---|
| 0 (start) | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 |
Growth Factor
A constant factor can be obtained by dividing each successive y-value by the previous y-value. This ratio is called the growth factor of the pattern.
Example
For each good-work day, the reward doubles. You multiply the previous award by 2 to get the new reward. This constant factor can also be obtained by dividing successive y-values: 2/1 = 2, 4/2 = 2, etc
Exponential Equation
Examining the growth pattern leads to a generalization that can be expressed as an equation.
An exponential growth pattern y = a(b)x may increase slowly at first but grows at an increasing rate because its growth is multiplicative. The growth factor is b.
Example
| Day | Calculation | Reward (cents) |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 x 2 = 21 | 2 |
| 2 | 1 x 2 x 2 = 22 | 4 |
| 3 | 1 x 2 x 2 x 2 = 23 | 8 |
| : | : | : |
| 6 | 1 x 2 x 2 x 2 x 2 x 2 x 2 = 26 | 64 |
| : | : | : |
| n | 1 x 2 x 2 x ... x 2 = 2n | 2n |
On the nth day, the reward R will be R = 1 x 2n. Because the independent variable in this pattern appears as an exponent, the growth pattern is called exponential. The growth factor is the base 2. The exponent n tells the number of times the 2 is a factor.
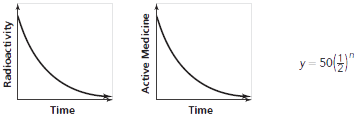
Exponential Decay
Exponential models describe patterns in which the value decreases. Decay factors result in decreasing relationships because they are less than 1.
Example
Rules of Exponents
Students begin to develop understanding for the rules of exponents by examining patterns in a powers table for the first 10 whole numbers.
Example
By examining the multiplicative structure of the bases:
82 = (2 x 2 x 2)2 = (23)2 = 26; the general pattern is (bm)n = bmn
9 x 27 = 243 or 32 x 33 = 35; in general, (bm)(bn) = bm+n
4 x 25 = 22 x 52 = (2 x 5)2 = 102 = 100; in general, (ambm) = (ab)m
Similar explorations lead to the rule am/an = am-n.