Preparing the Classroom Environment

As you prepare your classroom space, consider the following questions:

• How can I foster opportunities for student collaboration by arranging their seating?
• How can I ensure that there is room for students to move comfortably in the classroom?
• Where can I place the tools that students may need so that they are easily accessible? (calculators, rulers, angle rulers, grid paper, technology applets, and so forth)
• What is the best location for student materials? (scissors, markers, colored pencils, glue sticks, construction paper, chart paper, and so forth)
• How can I use wall space to display artifacts of student learning that will foster continued growth in our knowledge of mathematics?
• Where can we keep a record of our learning and the unresolved questions posed for further thinking during a Unit? During the school year?

Suggestions for Seating Arrangements for Various Groupings

Students often explore daily Problems individually, with a partner, or with a small group of 3 or 4 students. Therefore, having flexible seating for ease in grouping is effective.

To facilitate discussion and analysis of the mathematics, students and groups should display their thinking, including their conjectures and evidence to support or contradict them. Arranging student seating so that learners can move freely to post, analyze, and discuss their work is helpful.

As you determine where materials and tools will be located, remember that students should be able to move freely and have the freedom to choose which tools and materials to use as they delve into a Problem.

Suggestions for the Walls of a Classroom

• Post the Mathematical Goals (or the Mathematical Highlights) so that students may refer to them as they work through a Unit.
• Post the Standards for Mathematical Practices and Habits of Mind for students to refer to during the Summarizes and the Reflections.
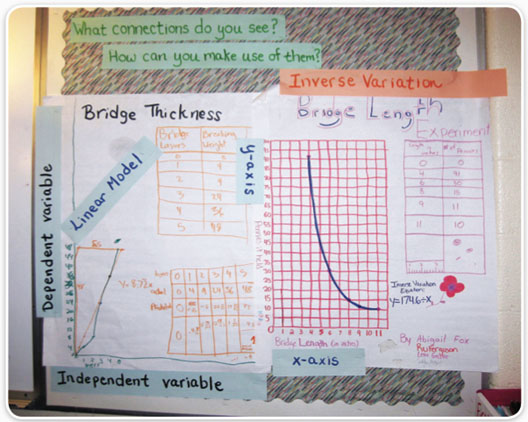
• Add vocabulary terms to visual representations of student work as the terms are formally developed during class. For example, when students make a graph from the bike tour in Variables and Patterns, place the terms independent variable and dependent variable along the x-axis and the y-axis.
• Post vocabulary terms as they are introduced and developed, making a word wall poster for each Unit.
• Make a memory wall to display key visual displays of learning from each Unit. Post the questions “What connections do you see?” and “How can you make use of them?” (See description below.)

The idea behind a memory wall is that the classroom should reflect students’ mathematical journey toward deeper understanding. Over the course of a Unit, students will benefit from having a visual reference. As the Unit draws to a close, students can select which visual display best represents their learning. Initially teachers may make those selections with the knowledge of what comes next.

You can post documentation on the walls of the sorting of polygons, data from testing triangle lengths with polystrips, and tiling designs showing those polygons that do and do not tile. The answer to each of these questions provides leverage for an upcoming Unit. In Stretching and Shrinking as students encounter rep-tiling in Investigation 3, they can compare and contrast tiling with rep-tiling] On the memory wall, students display their work from Shapes and Designs. This includes their predictions, testing, and data gathering to justify or contradict their predictions. Students later draw upon this work in Stretching and Shrinking.

As the memory wall becomes crowded, students can be asked to narrow down the artifacts to one display for each Unit after considering the question, “Which Problem displayed shows the big ideas that you want to remember?”