Comparing and Scaling

Revision Comments

There are 3 Investigations with 10 problems, the same as in CMP3. But this Unit takes advantage of the deeper development of proportional reasoning, or ratio reasoning, in the 6^th grade Comparing Quantities Unit and in the prior 7^th grade Stretching and Shrinking Unit. Thus, the development is deeper with the focus on recognizing and analyzing proportional relationships and using them to solve a variety of problems.

TOP OF PAGE

CMP STEM Problem Format

What is a CMP STEM Problem?

In CMP, the class discussions attend to three important features of the goal for a mathematics problem: (1) student strategies and problems solutions, (2) the embedded or encoded mathematics of the problem, and (3) connections to prior learning and future knowledge. To continue to support these discussions, the CMP problems have been newly designed to support STEM education. Rather than using conventional numbering and lettering (e.g., A1, A2, B1, B2, B3, etc.), the CMP problems now use three important components.

What are the components of a CMP STEM problem?

Why do CMP STEM Problems matter?

Often STEM professionals work to solve problems and meaningfully connect these solutions to inform the needs of society. The complexities of the world today necessitate that each and every student be prepared with the knowledge and skills to solve difficult problems, gather and evaluate evidence, and make sense of information. To promote learning that resembles the work of STEM professionals, the problems in CMP are redesigned using the new format to help produce a population of students that is more reflective of the wider STEM community.

How does the Launch-Explore-Summary instructional model connect to the CMP STEM Problems?

While CMP STEM Problems contain Initial Challenge, What If…? and Now What Do You Know components, the instructional model of Launch/Explore/Summary continues to be critical for CMP STEM Problems. In some ways, the Initial Challenge can be thought of as the box questions in CMP3. In the Launch, all three components are launched. There may be an occasion where teachers will want to have a brief summary before students go to the What If…? component. These are indicated in the teacher materials. The Now What Do You Know is intended for students to reflect on and be prepared to talk about what they have learned in the Summary. A teacher may choose to have students record some of their understandings in a “learning log” at the end of the Summary. These may be useful when students complete the Mathematical Reflections.

How do the Mathematical Reflections connect to the CMP STEM Problems?

The Mathematical Reflections build on the Now What Do You Know of each problem in the unit. Rather than having a Mathematical Reflection with different questions for each Investigation, the Mathematical Reflections are now streamlined around one essential question. For example, the Mathematical Reflection for each Investigation in Stretching and Shrinking: Developing Proportional Reasoning in the Context of Similarity (Scale Drawings) is:

View PDF

TOP OF PAGE

Unit Descriptions

Many quantitative problems can be solved simply by counting members of a set or by measuring segments, areas, volumes, angles, masses, or temperatures. However, it is often necessary to make decisions that involve comparisons of counts or measurements. The basic step in this way of thinking is developed in elementary grades. During these years, such comparisons are often made by deciding which number is greatest. More useful reasoning often requires more careful comparison—explaining how much greater one number is than another, not in an absolute sense, but in a relative sense.

When comparing the distance or difference between two numbers, we are using additive thinking such as that developed in Accentuate the Negative and in several of the CMP 6^th grade number Units. We can also compare two numbers by asking how many times greater one number is than another. When we do this, we are using multiplicative thinking, much of which was developed in the 6^th grade Prime Time and Comparing Quantities Units, as well as in the 7^th grade Accentuate the Negative and Stretching and Shrinking Units. Multiplicative thinking examines how many times greater one number is than another number. Multiplicative thinking also asks what fraction one number is of another number. There are many ways to make comparisons—fractions, ratios, rates, differences, and percents. Building on the reasoning with ratios in 6^th grade, one of the fundamental goals of school mathematics, especially middle grades mathematics, is to help students develop flexible understanding, skill, and disposition in using strategies for comparing quantities. This runs throughout the Problems, ACE Exercises, and Mathematical Reflection of Comparing and Scaling. This Unit confronts students with a series of mathematical tasks that encourage them to make decisions about the quantities relevant to each task, how those quantities can be compared most usefully, and what information is provided by various quantitative comparisons.

The second major theme of this Unit, as the title suggests, is scaling. In its most familiar sense, scaling suggests making something larger or smaller, but similar in key respects to an original. Ratios and fractions often express comparative information in scaled-down form. For example, if a class consists of 15 boys and 10 girls, we might say that the ratio of boys to girls is 3 to 2 or that 3 out of 5 students in the class are boys. We could also say that 60% of the class is boys, a kind of scaling up, from 3:5 to 60:100.

Comparing Quantities lays the foundation for supporting scaling with quantities. Stretching and Shrinking lays a solid foundation of visual imagery to support the basic notion of scaling. The idea of ratio comparison was introduced in these two Units, along with informal ideas of equivalent ratios. These ideas are extended in the current Unit. In addition, rate is defined as a special type of ratio that compares two measurements with different units.

In Stretching and Shrinking, the goal was to find dimensions of a larger (or smaller) physical or graphical model of some situation while preserving the relative size of the component parts so that the figures remained mathematically similar. The same ideas and ways of thinking developed in Stretching and Shrinking become powerful ways of thinking about ratios in Comparing and Scaling. The goal is the same in many ratio situations—to scale the ratios up or down to determine whether they are the same or different.

Another way the more numerical situations in Comparing and Scaling relate to the more geometric ideas in Stretching and Shrinking is that comparison problems often call for finding the missing part of a ratio equivalent to a given ratio, which is the same as solving a proportion. For example, suppose you have a rectangle with dimensions of 5 cm by 7 cm. You want to draw a larger, similar rectangle with the dimension corresponding to 5 cm being 15 cm. What would the other dimension be? This is the same as the question: If roses are 5 for $7 and I want to buy 15 roses, how much will they cost? In each case, we are dealing with the given ratio of 5 to 7 and looking for the equivalent ratio of 15 to x. Stretching and Shrinking precedes Comparing and Scaling to give students prior experience with these ideas in a more concrete geometric context.

To summarize, the broad purposes of this Unit are to deepen students’ ability to make intelligent comparisons of quantitative information—using ratios, fractions, decimals, rates, unit rates, and percents—and to use quantitative comparison information to make larger or smaller scale models of given situations or to scale rates and ratios up and down as needed. An additional goal of this Unit is to have students not only learn different ways to reason in proportional situations, but also recognize when such reasoning is appropriate.

Many important mathematical applications involve comparing quantities of one kind or another. In some cases, the problem is simply deciding which of two quantities is greater and describing how much greater it is. In such instances, we subtract to find a difference. This is what students deal with in elementary school. In fact, since situations that call for comparison by addition or subtraction come first in students’ experiences with mathematics, for many students this way of thinking becomes inappropriately pervasive in any situation requiring comparison.

As with all of the CMP4 Units, one Mathematical Reflection guides the development of the understanding of the mathematical ideas in the Unit.

Mathematical Reflection

In this Unit and in prior Units you have you have been exploring problem situations that require proportional reasoning. At the end of this Unit,

What does it mean to reason proportionally?

TOP OF PAGE

Summary of Investigations

Investigation 1: Proportional Reasoning Using Ratio Comparisons

Investigation 1 focuses on different strategies for comparing quantities—using ratios, fractions, and percents. Students learn what different types of comparative statements say about the given data. They are asked to write comparative statements using ratios and differences that describe data. In Problem 1.1 a context of various orange juice recipes raises the important question of how you decide whether to use a difference, ratio, fraction, or percent to make a particular comparison. In Problem 1.2 students use a variety of strategies for making comparisons and identify how information in each of these forms provides the information needed to derive any of the other forms. In Problem 1.3 students build on their prior understandings of proportional relationships to recognize and represent proportional relationships in new situations. They continue to strengthen their understanding of how ratios can be formed and scaled up or down to find equivalent ratios.

Investigation 2: Proportional Reasoning Using Rate Comparisons

Students continue to explore situations that require them to recognize and analyze proportional relationships and use these to solve problems. There are many different ways to make comparisons. In this Investigation, students isolate ratios and rates as being useful comparisons for a variety of situations. The situations in this Investigation motivate students to find and use unit rates. They then compare unit rates within a problem to decide which option is best. Unit rate and the constant of proportionality are recognized in contextual situations, tables, graphs, and equations, and are used to solve problems. Students can use other strategies to solve problems as well, such as rate tables, equations, and graphs. In Problem 2.1 students encounter deciding which table to sit at when the number of seats and amount of pizza are different at each table. Students use ratios to make their decision. In Problem 2.2 students investigate rates and rate tables using the price of pizza at different restaurants. In Problem 2.3 students look at unit rates and the constant of proportionality in several contexts on purchasing items.

Investigation 3: Pulling it all Together: Ratios, Rates, and Percent

In this Investigation, students use various proportional reasoning strategies they developed in Investigations 1 and 2 and apply those strategies in different contexts. Specifically, Problem 3.1 provides a consumer math context, an important real-world application of proportional reasoning. Problem 3.2 is a context in a restaurant where students encounter percents and discounts. Problem 3.3 is a situation involving a recipe to feed chimps that is given in percentages and needs to be scaled for specific situations. Problem 3.4 is a simulation experiment of a leaking faucet to pull together the ideas on proportions in this Unit.

TOP OF PAGE

Goals of the Units

Reasoning Proportionally: Develop and use strategies for solving problems that require proportional reasoning

• Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem
• Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations of quantitative data for correctness and quality
• Recognize proportional situations where percents or rates are the appropriate form of comparison
• Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation
• Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation
• Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation
• Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios
• Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units

TOP OF PAGE

Unit Alignments: Goals, CCSM, Arc Of Learning, Emerging Mathematics

INV 1 | INV 2 | INV 3

Investigation 1: Proportional Reasoning Using Ratio Comparisons

Students will be working to develop elements of the following Unit goals throughout Investigation 1.

Reasoning Proportionally: Develop and use strategies for solving problems that require proportional reasoning

• Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem
• Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations of quantitative data for correctness and quality
• Recognize proportional situations where percents or rates are the appropriate form of comparison
• Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation
• Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation
• Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation
• Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios
• Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units

1.1 Mixing Juice: Choosing a Comparing Strategy

1.2 TIME TO CONCENTRATE: SCALING RATIOS

1.3 Keeping Things in Proportion: Using Proportions

Mathematical reflection

Investigation 2: Proportional Reasoning Using Rate Comparisons

Students will be working to develop elements of the following Unit goals throughout Investigation 2.

Reasoning Proportionally: Develop and use strategies for solving problems that require proportional reasoning

• Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem
• Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations of quantitative data for correctness and quality
• Recognize proportional situations where percents or rates are the appropriate form of comparison
• Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation
• Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation
• Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation
• Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios
• Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units

2.1 Sharing Pizzas: Comparing Rate Strategies

2.2 Comparing Pizza Prices: How Do We Know It Is Proportional?

2.3 Finding Costs: Unit Rate and Constant of Proportionality

Mathematical Reflection

Investigation 3: Pulling It All Together: Ratios, Rates, and Percents

Students will be working to develop elements of the following Unit goals throughout Investigation 3

Reasoning Proportionally: Develop and use strategies for solving problems that require proportional reasoning

• Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem
• Represent proportional relationships with comparison statements, tables, graphs, and equations and analyze these representations about quantitative data for correctness and quality
• Recognize proportional situations where percents or rates are the appropriate form of comparison
• Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation
• Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation
• Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation
• Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios
• Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units

3.1 Using Percents: What is the Tax?

3.2 Using Percents: What is the Tip?

3.3 Free Throws and Deeding Chimps: The Percent Connection

Mathematical Reflections

Assessments

Check-Up

Question	CCSS(s)	Unit Goal(s)	Problem(s)
1	7.RP.A.1 7.RP.A.2B	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality	1.1 1.2 1.3
2	7.RP.A.1 7.RP.A.2	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality	1.1 1.2 1.3

Partner Quiz

Question	CCSS(s)	Unit Goal(s)	Problem(s)
1a	7.RP.A.1 7.RP.A.2	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison	2.1 2.2 2.3
1b	7.RP.A.1 7.RP.A.2 7.RP.A.3 7.EE.B.3	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	2.1 2.2 2.3
1c	7.RP.A.1 7.RP.A.2 7.RP.A.3 7.EE.B.3	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	2.1 2.2 2.3
1d	7.RP.A.1 7.RP.A.2 7.RP.A.3 7.EE.B.3	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	2.1 2.2 2.3
2	7.RP.A.1 7.RP.A.2 7.RP.A.2.A 7.RP.A.2.B 7.RP.A.3 7.EE.B.4	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation	2.2 2.3
3	7.RP.A.2.B	Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation	2.3
4	7.RP.A.1 7.RP.A.2 7.RP.A.2.A 7.RP.A.2.B 7.RP.A.2.C 7.RP.A.2.D 7.RP.A.3 7.EE.B.3 7.EE.B.4 7.EE.B.4.A	Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations, and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios	2.1 2.2 2.3

Unit Test

Question	CCSS(s)		Unit Goal(s)	Problem(s)
1	7.RP.A.1 7.RP.A.2 7.RP.A.2.B		Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	1.1 1.2 1.3 2.1 2.3
2	7.RP.A.1 7.RP.A.2 7.RP.A.2.A 7.RP.A.2.B 7.RP.A.2.C 7.RP.A.2.D 7.RP.A.3 7.EE.A.2 7.EE.B.3 7.EE.B.4 7.EE.B.4.A		Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Recognize that constant growth in a table, graph, or equation is the constant unit rate associated with the proportional situation Relate the unit rate and constant of proportionality to an equation, graph, or table describing a proportional situation Relate what a point (x, y) on the graph of proportional relationship means in terms of the situation and how this information is also represented in a table or graph of the situation Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	1.1 1.2 1.3 2.1 2.2 2.3 3.1 3.2 3.3 3.4
3	7.RP.A.3 7.EE.B.3		Recognize proportional situations where percents or rates are the appropriate form of comparison Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	3.1 3.2
4	7.RP.A.2 7.RP.A.3 7.EE.B.3		Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Recognize proportional situations where percents or rates are the appropriate form of comparison Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	1.1 1.2 1.3 2.1 3.4
5	7.RP.A.1 7.RP.A.2 7.RP.A.3		Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Represent proportional relationships with comparison statements, tables, graphs, and equations and analyze these representations about quantitative data for correctness and quality Recognize proportional situations where percents or rates are the appropriate form of comparison Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	1.2 2.1 2.3 3.4
6	7.RP.A.2 7.RP.A.3 7.EE.B.3		Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Recognize proportional situations where percents or rates are the appropriate form of comparison Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	3.1 3.2
7	7.RP.A.2 7.RP.A.3 7.EE.B.3		Recognize and analyze situations in which proportional reasoning is appropriate to solve the problem Recognize proportional situations where percents or rates are the appropriate form of comparison Use various strategies to solve for an unknown in a proportion, including scaling, rate tables, percent bars, unit rates, and equivalent ratios Set up and solve proportions that arise from real-world applications, such as finding discounts and markups and converting measurement units	3.1 3.2

TOP OF PAGE

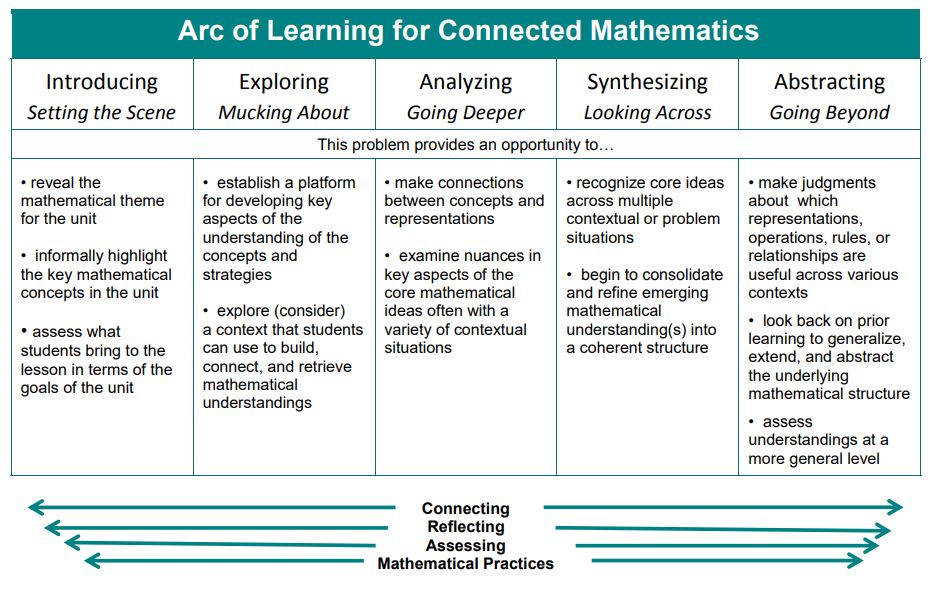
General Arc of Learning

View Arc of Learning PDF

TOP OF PAGE

Unit Arc of Learning

The purpose of this Unit is to develop students’ abilities to make intelligent comparisons of quantitative information – using ratios, fractions, decimals, rates, unit rates, and percents – and to use quantitative information to scale rates and ratios up and down as needed. Students not only learn different ways to reason in proportional situations, but also to recognize when such reasoning is appropriate. Developing proportional reasoning starts with the 6^th grade Comparing Quantities Unit and surfaces throughout the rest of the 6^th grade Units. Thoroughly understanding and skillfully using proportional reasoning means that students need to explore it in many different contexts, recognizing when it is appropriate and when it is not. In 7^th grade proportional reasoning is the backbone of most of the Units. For example, similar figures or scale drawings provide a geometric context for exploring proportional reasoning in the Stretching and Shrinking Unit. It surfaces in the Moving Straight Ahead Unit as students explore linear situations, some of which are proportional, and some of which are not. It is also the backbone for the How Likely Is It? Unit to explore probability situations. It surfaces again in the Filling and Wrapping and Samples and Population Units. Proportional reasoning by definition is done within the context of other mathematical strands: geometry, number, probability, data, and functions.

View as PDF

TOP OF PAGE

Mathematical Overview

Mathematics Overview: Comparing and Scaling

Key ideas: Ratio, Rate, Percent

Major Focus: Proportional Reasoning

Strategic Connections: Algebra

Comparing and Scaling is the third Unit in CMP that is focused, almost exclusively, on proportional reasoning. Ratios, equivalent ratios, and unit rates were introduced in 6^th grade in Comparing Quantities, and reinforced in other 6^th grade Units, Let’s Be Rational 1 and 2 and Data About Us. In 7^th grade Stretching and Shrinking investigates what proportional reasoning means in geometric situations, and the ideas of scaling and scale factor are introduced in terms of scaling up or down a geometric figure. In Comparing and Scaling, unit rate is prominent, and students learn how unit rate is integral to the tables, graphs, and equations representing proportional relationships. Students are encouraged to look for similarities across multiple contexts, and to recognize proportional situations in any representation. Proportions* are solved using various strategies, reflecting students’ familiarity with ratios and rate tables. Non-proportional situations are introduced to strengthen students’ sense of a proportional relationship.

LINK TO THE FUTURE: Later in 7^th grade the Unit Moving Straight Ahead explores linear relationships. Some of these linear relationships are proportions and some are not. The contrast will be made. In addition, in 8^th grade inverse variation will be contrasted with proportions.

In roughly this order, students:

• Analyze when a situation is proportional and when it is not,
• Represent proportional relationships, using tables, graphs, and equations,
• Recognize when a table, graph or equation represents a proportional situation,
• Relate unit rate in proportional situations to constant of proportionality on a graph, to the coefficient of x in the form y = mx, or to the ratio y/x = m/1,
• Connect percent relationships to proportional reasoning,
• Solve problems (throughout the Unit) in various contexts, including discounts and markups, using various strategies, including scaling, graphing, unit rates, and proportions.

*Note: Teachers may recall solving proportions by “cross-multiplying.”  CMP does not recommend that you teach this. It looks like this:

Notice that the final result of this technique is 4 multiplied by 57 and divided by 10. To get to this result there is a middle line where the units are not meaningful, “somethings.” It is not shorter or more efficient than dividing by 10 to get the unit rate of pizzas per camper, and then multiplying by 57, to scale up to 57 campers.

The same operations are applied but by scaling the units remain meaningful throughout. Student strategies should always make sense. (See Proportions in this overview.)

Proportional Relationships: How to represent them, how to recognize them, the role of unit rate

Recognizing Proportional Relationships from Representations

From the Context

What all proportional situations have in common is a multiplicative comparison. For example, in the orange juice recipes pictured below, when we think about which recipe is more orangey we do not look at the difference between 2 cups of concentrate in Recipe A and 5 cups of concentrate in Recipe B or the difference between amounts of concentrate and amounts of water within each recipe. We compare ratios, 2:3 in Recipe A and 5:9 in Recipe B. We think of how many times bigger 3 is than 2, or 9 is than 5. (We may also use a unit rate to make the comparison. (CAUTION: Rates also appear in non-proportional situations. See non-example.)

 

From the Table

The multiplicative comparison (and the unit rate) become apparent when the data about a recipe is put into a table. Data for Recipe A is shown in the following table.

Cups Concentrate	2	4	6	8	…	?
Cups Juice	5	10	15	20	…	240

Looking vertically in the table at the ratio 2 : 5, and all the other equivalent ratios, 4  :10, 6 : 15 etc, the amount of juice is always 2.5 times the amount of concentrate. 

Cups Conc.	2	4	6	8	…	?
Cups Juice	5	10	15	20	…	240

We can skip to 240 cups juice and divide this by 2.5 to find the cups of concentrate needed. (2.5 is also a unit rate. See Unit Rate.)

Looking horizontally at the ratios 2 : ? and 5 : 240, we can ask by how much we should multiply or scale up 5 cups of juice to make 240 cups.

Cups Concentrate	2	4	6	8	…	?
Cups Juice	5	10	15	20	…	240

Then, do the same to 2 cups of concentrate.

From the Graph

The graph of a proportional relationship is a straight line that passes through the origin. The point (0, 0) must be on the graph; for example, with 0 cups of concentrate we make 0 cups of juice.

From the Equation

The equation of the line shown is J = 2.5C.  The equation tells us that to get the number of cups of juice (J), we have to multiply the number of cups of concentrate (C) by 2.5. This is what the vertical ratio comparison in the table tells us. The coefficient of C in the equation is 2.5. This is the unit rate, 2.5 cups of juice for every 1 cup of concentrate. It is called the constant of proportionality.

Unit Rate

Proportional relationships always include a unit rate. The unit rate is recognizable in all representations and plays a role in solving problems.

In the Table: Students know from Comparing Quantities that there are two unit rates.

Cups Concentrate	0.4	1	2	…	?
Cups Juice	1	2.5	5	…	240

2 : 5 = 1 : 2.5 = 0.4 : 1. 

For every 1 cup of concentrate there are 2.5 cups juice. For every 0.4 cups of concentrate there is 1 cup of juice. 

The unit rate is derived from the vertical ratio in the table.

When the table includes all whole number values for one of the two quantities in the ratio, as below, you can see the unit rate as the rate of change.  (This relates to the idea of slope, which is explored in Moving Straight Ahead.)

Cups Concentrate	1	2	3	4	…
Cups Juice	2.5	5	7.5	10	…
Cups Concentrate	0.4	0.8	1.2	1.6	…
Cups Juice	1	2	3	4	…

In the Graph

The unit rate is visible in the graph as the “steps.” For a proportional relationship, the unit rate is the rate of change that determines the slope of the line. It shows visually that for every 1 cup of concentrate we have 2.5 cups of juice or for every 1 cup of juice we have 0.4 cups of concentrate.

In the Equation

There are two equivalent equations for this situation.

J = 2.5 C. Also, C = 0.4 J. It depends on which information we are given or which one is more convenient to use.  If we are given J = 240, we can either solve 240 = 2.5C, or C = 0.4(240).

Non-Example

Curriculum decision: Non-examples help to clarify how to distinguish a proportional relationship from a non-proportional relationship.

If 15 pizzas cost $165 then each pizza costs $11. BUT there is a delivery charge of $30.

Number 1 2 3 … 15 Cost 11 + 30 22 + 30 33 + 30   165 + 30

In the Context: There is a rate per pizza of $11 : 1 pizza, but the delivery cost adds to the cost, so the overall unit rate changes per pizza delivered.

In the table: When delivery is included the vertical ratios are

 

The first horizontal ratios are 

Neither the horizontal nor vertical ratios are equal.

Note: The rate of change can be seen in the table, but not as a multiplicative comparison with the ratios.

On the Graph: The graph is linear but does not pass through the origin. (0, 30) on the graph indicates that even for 0 pizzas the delivery charge is $30.

In the equation: C = 11N + 30. The additive term (+30) means this is not a proportional relationship.

Strategies: Solving problems about proportional situations

Tables, Scaling, Equivalent Ratios, Unit Rate

We can use tables, graphs, and equations to solve problems about proportional situations.

Suppose the problem is to figure out how many pizzas we should order for 240 campers, when 4 pizzas serve 10 campers, as shown in the graphic.

Scaling a ratio

The vertical ratios are all equal in the table of a proportional relationship. We can scale up 4:10.

Multiplying by a scale factor of 24, we have 4:10 = 96 : 240. We need 96 pizzas.

Scaling a unit rate

This is a variation of scaling a ratio.

Find the number of pizzas for 1 camper by scaling 4:10 down to 0.4: 1. Then scale up the unit rate.

Note: There are two unit rates, 2.5 campers per 1 pizza, and 0.4 pizzas per 1 camper.

The latter is more convenient for scaling up the number of campers from 1 to 240.

Using a graph

We can graph the data using data from the table, (4, 10), (8, 20), (12, 30) etc., and extend the line to find the point (P, 240).

Using an equation

The unit rate is 0.4 pizzas (P) per 1 camper (C). The equation is P = 0.4C.

 If C = 240, then P = 0.4(240) = 96.

Note: From the table of ratios, we can say 

P:C = 0.4:1.

Or writing this in fraction format

This is equivalent to P = 0.4C.

In general, a proportional relationship can be represented by an equation of the form y = mx, or y/x = m/1, where m is the unit rate or the constant of proportionality.

Proportions

A proportion is an equality between two ratios written in a fraction format. The problem about sharing pizzas among campers can be solved various ways by using tables, or by explicitly stating the proportion below.

Note: We can write this proportion in equivalent ways.

These equal ratios appear in the table comparing number of pizzas and number of campers.

Let’s change the numbers to demonstrate that scaling and unit rates always work to solve proportions. Let’s suppose we have to solve

One way to do this is by scaling 4/10 down to 0.4/1 by dividing by a factor of 10 as below.

Now scaling up 0.4/1 by multiplying by a factor of 57 we have

So, P = 0.4 (57) = 22.8. (Better order 23 pizzas.)

Students will have variations on this proportional reasoning. It is a natural outgrowth from familiarity with rate tables and equivalent ratios.

Percent problems

Percent problems are examples of proportional situations, since P% is a ratio P:100. Students have represented these with percent bars/tape diagrams and ratios in previous Units. They can write and solve them as proportions now.

The graphic below shows a percent bar and parts of tables. It asks What is x, given x is 40% of 180? Or, if the sale price is 40% of the original $180, what is the sale price?

The graphic below illustrates What is x, if x is 128% of 45? Or, if the markup is 28% on a buying price of $45, what is the selling price?

The graphic below illustrates What percent is 170 if 190 is 100%? Or, if $190 is the original price and the discounted price is $170, what was the percent discount?

Percent bars and tables and proportions can be used to represent and solve any percent problem.

TOP OF PAGE

Learning Aid

• 1.1 Strategies
• 1.2 Recipes
• 2.1A Pizzas and Tables
• 2.1B Strategies
• 2.2 Royal and Howdy Pizza Costs
• 2.3 Cost of Oranges
• 3.1A Cost of Skylar's School Items
• 3.1B Student Strategies
• 3.2 Larry's Lunch Place Menu
• 3.3 Chimp Food Mixtures
• 3.4 Leaky Faucet Data

TOP OF PAGE

Teaching Aids

• 1.1 Orange Juice Recipes
• 1.2 Ratio Types Notation
• 1.3 Proportional Reasoning Examples
• 3.1 Introduction
• 3.4 Leaky Faucet Experiment Directions

Family Letter

View Family Letter.

Assessments

• Check Up 1
• Partner Quiz
• Unit Test

Applications-Connections-Extensions (ACE) Homework

• ACE without answers
• ACE with answers

© 2022 Connected Mathematics Project at Michigan State University
Do not copy, share, or duplicate without permission.