Stretching and Shrinking
Revision Comments
The following changes were made to Stretching and Shrinking from the CMP3 to CMP4.
- Investigation 1 has three Problems rather than two. The Mystery Teacher has been elevated to a Problem to emphasize the pre-assessment embedded in this informal introduction to similarity. Allowing teachers to assess what knowledge of proportional reasoning students bring to the Problem.
- Investigation 2 is the same mathematical content with three Problems.
- Investigation 3 has three rather than four Problems. The first two Problems on rep-tiles have been combined. Students investigate both rep-tiling with triangles and quadrilaterals. The teacher may choose to have different groups work on triangles and other groups work on quadrilaterals. Alternately, each group could do 1-2 triangles and 1-2 quadrilaterals.
- Investigation 4 has three Problems rather than four. The first two Problems combine parallelograms and triangles which can be done by everyone. Alternately the teacher may assign one group of parallelograms and one group of triangles to some groups with the other groups of parallelograms and triangles assigned to the rest of the groups.
- Some titles and subtitles have been changed to reflect CCSSM such as the major role that proportional reasoning plays in developing understanding of similar figures (scale drawings).
CMP STEM Problem Format
What is a CMP STEM Problem?
In CMP, the class discussions attend to three important features of the goal for a mathematics problem: (1) student strategies and problems solutions, (2) the embedded or encoded mathematics of the problem, and (3) connections to prior learning and future knowledge. To continue to support these discussions, the CMP problems have been newly designed to support STEM education. Rather than using conventional numbering and lettering (e.g., A1, A2, B1, B2, B3, etc.), the CMP problems now use three important components.
What are the components of a cmp stem problem?
Problem
Initial Challenge
Component Description
The Initial Challenge contextualizes the problem and presents the challenge. The IC also provides an opportunity for open access to the mathematical challenge of the problem.
What If...?
The What If…? unpacks the embedded or encoded mathematics of the problem. The WI…? provide students with further opportunities to probe at the mathematics. Situations focus on what happens when you consider changed quantities or parameters, new aspects to the context, or returning to mathematical ideas mentioned earlier. Situations also focus on different solution strategies and work that students can do to solve the problem.
Now What Do You Know?
The Now What Do You Know connects learning to prior knowledge and consider future payoffs. As with the Focus Questions in the CMP3 Teacher’s Guide, the NWDYK provides focus on the learning goal of the mathematics problem. Whether students write answers is up to the teacher, but written and verbal discussions occur in the Problem Summary and in the Mathematical Reflections that span across problems.
Why do CMP STEM Problems matter?
Often STEM professionals work to solve problems and meaningfully connect these solutions to inform the needs of society. The complexities of the world today necessitate that each and every student be prepared with the knowledge and skills to solve difficult problems, gather and evaluate evidence, and make sense of information. To promote learning that resembles the work of STEM professionals, the problems in CMP are redesigned using the new format to help produce a population of students that is more reflective of the wider STEM community.
How does the Launch-Explore-Summary instructional model connect to the CMP STEM Problems?
While CMP STEM Problems contain Initial Challenge, What If…? and Now What Do You Know components, the instructional model of Launch/Explore/Summary continues to be critical for CMP STEM Problems. In some ways, the Initial Challenge can be thought of as the box questions in CMP3. In the Launch, all three components are launched. There may be an occasion where teachers will want to have a brief summary before students go to the What If…? component. These are indicated in the teacher materials. The Now What Do You Know is intended for students to reflect on and be prepared to talk about what they have learned in the Summary. A teacher may choose to have students record some of their understandings in a “learning log” at the end of the Summary. These may be useful when students complete the Mathematical Reflections.
How do the Mathematical Reflections connect to the CMP STEM Problems?
The Mathematical Reflections build on the Now What Do You Know of each problem in the unit. Rather than having a Mathematical Reflection with different questions for each Investigation, the Mathematical Reflections are now streamlined around one essential question. For example, the Mathematical Reflection for each Investigation in Stretching and Shrinking: Developing Proportional Reasoning in the Context of Similarity (Scale Drawings) is:
Mathematical Reflection
In this unit, we used proportional relationships to investigate similar figures or scale drawings, including how to determine if two figures are similar. In this Investigation,
What do you know about similarity? How were propotional relationships used to study similarity?
Unit Descriptions
Knowledge of similarity is important to the development of students’ understanding of the geometry in their environment. In their immediate environment and in their studies of natural and social sciences, students frequently encounter phenomena that require familiarity with the ideas of enlargement, scale factors, area growth, indirect measurement, and other similarity-related concepts. Similar figures are another name for scale drawings. In scale drawings, the original figure and its image are similar figures. In this unit we will use the two terms interchangeably.
Similarity is also a context in which students’ understanding of proportional reasoning continues to deepen. For example, if you increase the size of a diagram by 50%, then distances in the enlarged diagram are proportional to distances in the original diagram. Specifically, every distance in the enlargement is a constant multiple (1.5) of the corresponding distance in the original. It is generally recognized that understanding proportional reasoning is an important stage in cognitive development.
Students in the middle grades often experience difficulty with ideas of scale, which is the heart of proportionality. They confuse adding situations with multiplying situations. Situations requiring comparison by addition or subtraction come first in students’ experience with mathematics and often dominate their thinking about any comparison situation, even those in which scale is the fundamental issue. For example, when considering the dimensions of a rectangle that began as 3 units by 5 units and was enlarged to a similar rectangle with a short side of 6 units, many students will say the long side is now 8 units rather than 10 units. They add 3 units to the 5 units rather than multiply the 5 units by 2, the scale factor. These students may struggle to build a useful conception that will help them distinguish between situations that are additive and those that are multiplicative (calling for scaling up or down).
The Problems in this Unit are designed to help students begin to accumulate the knowledge and experiences necessary to make these kinds of distinctions and to reason about scaling in geometry situations. The next Unit, Comparing and Scaling, will continue to deepen their reasoning with proportions in the context of quantities. It develops these ideas in numerical, rather than geometric, contexts. Students develop understanding of what it means to be similar figures (scale drawings), this knowledge is required for students to be successful in the 8th grade unit, Flip, Spin, Slide, and Stretch
Mathematical Reflection
In this unit, we used proportional reasoning to solve problems involving similar figures (scale drawings). At the end of this Investigation,
What do you know about similar figures? What do you know about proportional reasoning?
Summary of Investigations
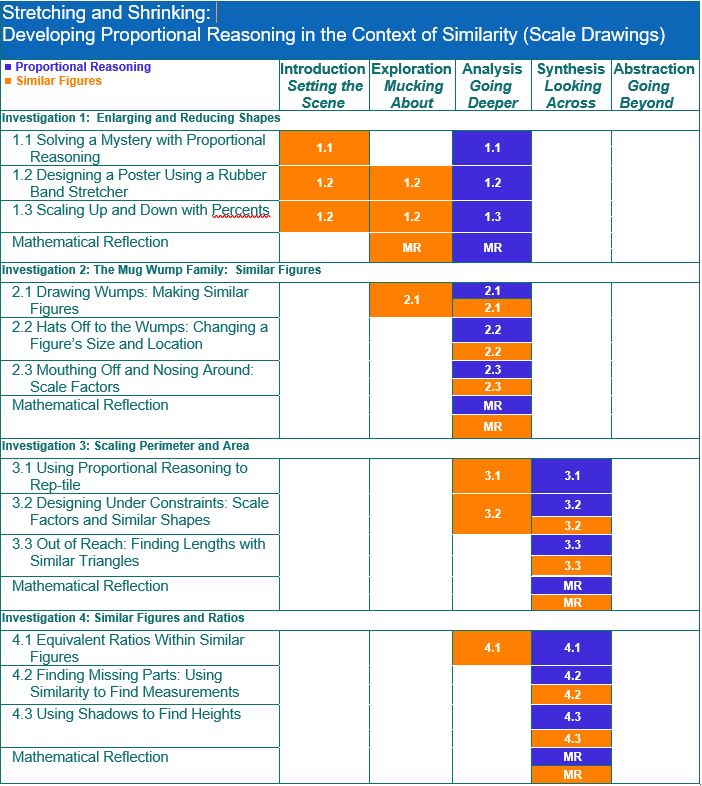
Investigation 1: Enlarging and Reducing Shapes
This Investigation informally introduces ideas about mathematical similarity by focusing on scale drawings. Students explore mathematical similarity by relating it to the use of the word similar in everyday life.
In Problem 1.1 students estimate the height of a mystery person in a picture by taking an actual measurement into account.
In Problem 1.2 students use rubber bands to enlarge a figure. Students compare how the general shape, lengths of line segments, areas, perimeters, and angles are affected.
In Problem 1.3 students investigate how a copy machine can produce similar figures both larger and smaller than the original. They use percents to compare the scale drawings.
Students explore similar figures in different sizes and compare changes in their side lengths, angle measures, perimeters, and areas. They determine which properties of a figure change and which properties remain the same when a figure is scaled up and down.
Investigation 2: SIMILAR FIGURES
Students build a good working definition of similarity in mathematical terms. Using the coordinate system, they draw several geometric figures representing characters called “Wumps.” They begin to see connections between geometry and algebra.
In Problem 2.1 students make similar and non-similar shapes using a coordinate system. Students graph characters called “Wumps” and find that Wump family members are similar to one another. They explore algebraic rules that cause images to change size. They also compare angle measures and lengths of corresponding sides informally as they investigate transformations.
In Problem 2.2 students explore algebraic rules that cause images to change size and to move about the coordinate plane. Students recognize the role that multiplication plays in scaled drawings, laying a foundation for students’ later work on proportional relationships in the Comparing and Scaling Unit.
In Problem 2.3 students are introduced to the term scale factor. Students find that for two figures to be similar, corresponding angles must be congruent; and corresponding sides must grow or shrink by the same factor, called the scale factor. They begin to recognize the role multiplication plays in similarity relationships.
Investigation 3: Scaling Perimeter and Area
During Investigation 3, students deepen their understanding of what it means for two figures to be similar.
In Problem 3.1 students experiment with rep-tiles, shapes where copies are put together to make larger, similar figures. Using rep-tiles, students explore the relationship between the areas of two similar figures. Students sometimes have difficulty grasping the idea that area does not grow at the same rate as side length when a figure is enlarged. Experiences with rep- tiles help them build mental images to support their evolving ideas about the relationship between scale factor and area.
In Problem 3.2 students use similarity and scale factors to find unknown measures or measures of distances that cannot be easily measured directly.
In Problem 3.3 students use similar triangles to measure distances on the ground that cannot be measure directly.
Investigation 4:Similarity and Ratios
Investigation 4 links scaled drawings to proportional reasoning.
In Problem 4.1 students use ratios to determine whether or not two figures are similar. They find ratios of two lengths within each figure, and then compare those ratios. Proportions are introduced as an equation stating that two ratios are equal.
In Problem 4.2 students use ratios and scale factors to find missing side lengths of similar figures. In Grade 6, students expressed ratios as comparison statements. In this Investigation, students extend their use of ratios by expressing ratios as fractions.
In Problem 4.3 students apply their knowledge of similarity to real-world problems. They use the shadow method to find heights of tall objects.
Goals of the Units
Similar Figures (Scale Drawings): Understand what it means for figures to be similar
- Identify similar figures by comparing corresponding sides and angles
- Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures
- Recognize the role multiplication (ratios), plays in similarity relationships
- Recognize the relationship between scale factor and ratio in similar figures (scale drawings)
- Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings)
Proportional Reasoning: Develop proportional reasoning strategies in the context of similar figures
- Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas
- Contrast proportionality in the context of geometry (similarity) with numerical situations
- Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities
- Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures
- Use similarity (scaling) to solve real-world problems
Unit Alignments: Goals, CCSM, Arc Of Learning, Emerging Mathematics
Investigation 1: Enlarging and Reducing Shapes
Students will be working to develop elements of the following Unit Goals throughout Investigation 1
Similar Figures (Scale Drawings): Understand what it means for figures to be similar
- Identify similar figures by comparing corresponding sides and angles
- Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures
- Recognize the role multiplication (ratios), plays in similarity relationships
- Recognize the relationship between scale factor and ratio in similar figures (scale drawings)
- Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings)
Proportional Reasoning: Develop proportional reasoning strategies in the context of similar figures
- Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas
- Contrast proportionality in the context of geometry (similarity) with numerical situations
- Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities
- Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures
- Use similarity (scaling) to solve real-world problems
1.1 Solving a Mystery with Proportional Reasoning
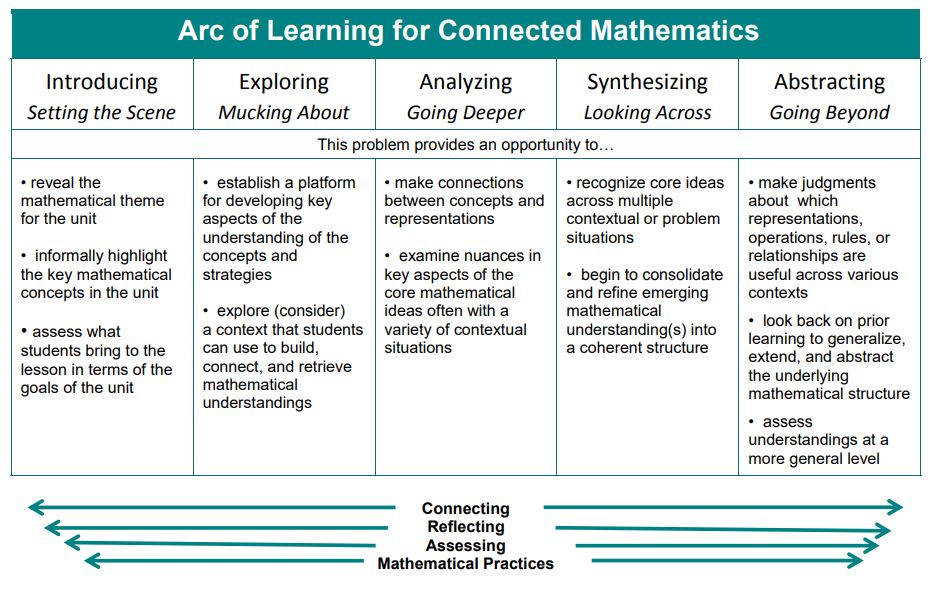
Arc of Learning
Introduce & Introduce/Explore
CCSSM
7.G.A.1, 7.RP.A.2, 7.RP.A.2.B
NWDYK
The Mystery Club advisor says that the picture is similar to the actual scene. What do you suppose the advisor means by similar? How is the photo similar to the actual scene that is photographed?Assume you continue to walk at the rate determined in the Initial Challenge. Describe in words the distance you could walk in a given number of seconds. Then write an equation to represent this information.
Emerging Mathematical Ideas
Build off the common language of “similar” to informally introduce the idea of two figures being mathematically similar.
Apply knowledge of ratios and begin to recognize proportional relationships between quantities to estimate length of enlarged figure.
1.2 DESIGNING A POSTER USING A RUBBER BAND STRETCHER
Arc of Learning
Introduction, Exploration, Analysis
CCSM
7.G.A.1, 7.RP.A.2, 7.RP.A.2.B
NWDYK
The original figure and its image are similar figures. The image is also called the scale drawing of the original figure. For two similar figures, what characteristics and measures are the same? Different? Explain how you know.
Emerging Mathematical Ideas
Informally explore enlarging a geometric figure and begin to notice which attributes change and which stay the same:
- angles of the two figures appear to be the same
- side lengths of the enlarged figure are longer
- area of the enlarged figure is bigger
1.3 scaling up and down with percents
Arc of Learning
Introduction, Exploration, Analysis
CCSSM
7.G.A.1, 7.RP.A.2, 7.RP.A.2.B
NWDYK
For similar figures, what features (attributes) and measures stayed the same? What features (attributes) and measures changed? How does a multiplier play a role in these changes?
Emerging Mathematical Ideas
Continue exploring enlargements and reduction of geometric figures, working to understand what attributes change and what attributes stay the same and by how much (the multiplier).
When exploring a set of geometric figures: original, an enlargement and a reduction, begin to use and articulate relationships between attributes, such as:
- corresponding angles of an enlargement or reduction of an original figure stay the same
- side lengths of an enlargement or reduction figure, as compared to the original figure, change in size by the multiplier used with the original
- perimeter of an enlargement or reduction figure, as compared to the original figure, changes in size by the multiplier used with the original
- area of an enlargement figure, as compared to the original figure, changes, but not by the multiplier used on the original figure; rather it grows by a greater factor than the multiplier
- area of a reduced figure, as compared to the original figure, changes but not by the multiplier used on the original figure; rather it shrinks by a greater factor than the multiplier
Mathematical reflection
Arc of Learning
Exploration & Analysis
CCSSM
Responses to the reflection are informed by the work in the Investigation and thus also reflect 7.G.A.1, 7.RP.A.2, 7.RP.A.2.B
Mathematical reflection
What do you now know about similar figures? What do you know about proportional reasoning?
Emerging Mathematical Ideas
Early exploration of proportional relationships between corresponding side length, perimeter, and area of similar figures.
When exploring a set of geometric figures including an original and enlargement or a reduction, begin to use and articulate relationships between attributes, such as:
- corresponding angles of an enlargement or reduction of an original figure stay the same
- side lengths of an enlargement or reduction figure, as compared to the original figure, change in size by the multiplier used with the original
- perimeter of an enlargement or reduction figure, as compared to the original figure, change in size by the multiplier used with the original
- area of an enlargement figure, as compared to the original figure, changes but not by the multiplier used on the original figure; rather it grows by a greater factor than the multiplier
- area of a reduced figure, as compared to the original figure, changes but not by the multiplier used on the original figure; rather it shrinks by a factor greater than the multiplier.
Investigation 2: The Mug Wump Family: Similar Figures
Students will be working to develop elements of the following Unit Goals throughout Investigation 1.
Similar Figures (Scale Drawings): Understand what it means for figures to be similar
- Identify similar figures by comparing corresponding sides and angles
- Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures
- Recognize the role multiplication (ratios), plays in similarity relationships
- Recognize the relationship between scale factor and ratio in similar figures (scale drawings)
- Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings)
Proportional Reasoning: Develop proportional reasoning strategies in the context of similar figures
- Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas
- Contrast proportionality in the context of geometry (similarity) with numerical situations
- Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities
- Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures
- Use similarity (scaling) to solve real-world problems
2.1 Drawing Wumps: Making Similar Figures
Arc of Learning
Exploration, Analysis, Analysis
CCSSM
7.G.A.1, 7.RP.A.2, 7.RP.A.2.B, 7.EE.B.4.A
NWDYK
How can you determine if an original figure and its image are similar by looking at the coordinate rule that produced the image? What features (attributes) stay the same for Mug and similar figures? What features change?
Emerging Mathematical Ideas
Explore enlarging geometric figures using coordinate grids and rules that produce both similar and non-similar figures. Expand understanding about which attributes change and which stay the same:
- corresponding angles of two similar figures are the same measure while angles of non-similar figures may not be.
- corresponding side lengths of the similar figure increases by the multiplier used to create a new rule.
2.2 Hats Off to the Wumps: Changing a Figure’s Size and Location
Arc of Learning
Analysis, Analysis
CCSSM
7.G.A.1, 7.G.B.6, 7.RP.A.2, 7.RP.A.2.B, 7.NS.A.2
NWDYK
If you know the coordinate rules to create an image, how can you tell if the two figures are similar? How can you use the rule to predict the side lengths of the image? How is the effect of a coordinate rule like the effect of a rubber band stretcher or a copy machine setting?
Emerging Mathematical Ideas
Continue to explore enlarging, shrinking, and moving geometric figures using coordinate grids and rules that produce both similar and non-similar figures, including multipliers that are rational numbers. Expand understanding of which attributes change and which stay the same:
- corresponding angles of two similar figures are the same measure while angles of non-similar figures may not be.
- corresponding side lengths of the similar figure increases or decreases by the multiplier used to create a new rule.
adding or subtracting numbers to a rule results in a figure moving on a grid but not in changing the shape or size of the new figure.
2.3 Mouthing Off and Nosing Around: Scale Factors
Arc of Learning
Analysis, Analysis
CCSSM
7.G.A.1, 7.RP.A.2, 7.RP.A.2.B
NWDYK
How can you decide if two shapes are similar? How can you determine the scale factor between two similar shapes?
Emerging Mathematical Ideas
Introduce the terms “scale factor” and connect it to “multiplier” to describe the relationship between corresponding side lengths of similar figures.
Use knowledge of scale drawings/similar figures to determine if any two rectangles or two triangles are similar.
Identify the scale factor of any two similar figures
Represent the relationship between corresponding sides of similar figures with a ratio.
Mathematical Reflection
Arc of Learning
Analysis & Analysis
CCSSM
Responses to the reflection are informed by the work in the Investigation and thus also reflect: 7.G.A.1, 7.G.B.6, 7.RP.A.2, 7.RP.A.2.B, 7.EE.B.4.A, 7.NS.A.2
Mathematical Reflection
What do you now know about similar figures? What do you know about proportional reasoning?
Emerging Mathematical Ideas
With similar figures, understand which attributes change and which stay the same:
- corresponding angles of two similar figures are the same measure while angles of non-similar figures may not be.
- corresponding side lengths of similar figures increase or decrease by the scale factor used to create an image.
- perimeter of a new similar figure, as compared to the original figure, changes in size by the scale factor between the original and the new image.
- Understand the relationship between corresponding sides of similar figures with a ratio.
Investigation 3: Scaling Perimeter and Area
Students will be working to develop elements of the following Unit Goals throughout Investigation 3.
Similar Figures (Scale Drawings):Understand what it means for figures to be similar
- Identify similar figures by comparing corresponding sides and angles
- Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures
- Recognize the role multiplication (ratios), plays in similarity relationships
- Recognize the relationship between scale factor and ratio in similar figures (scale drawings)
- Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings)
Proportional Reasoning: Develop proportional reasoning strategies in the context of similar figures
- Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas
- Contrast proportionality in the context of geometry (similarity) with numerical situations
- Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities
- Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures
- Use similarity (scaling) to solve real-world problems
3.1 Using Proportional Reasoning to Rep-tile
Arc of Learning
Analysis & Synthesis
CCSSM
7.G.A.1, 7.G.A.2, 7.RP.A.1
NWDYK
How do rep-tiles show the relationship between the scale factor and the perimeter and area of similar shape?
Emerging Mathematical Ideas
Explore enlarging a geometric figure using “rep-tiling. Expand understanding of similar figures and which attributes change and which stay the same:
- corresponding angles of two similar figures are the same measure while angles of non-similar figures may not be.
- corresponding side length of the rep-tile (similar figure) increases by the scale factor used to create a new figure.
- perimeter of the rep-tile (similar) figure increases by the scale factor
- area of the rep-tile (similar) figure increases by the scale factor squared.
3.2 Designing Under Constraints: Scale Factors and Similar Shapes (Scale Drawings)
Arc of Learning
Analysis, Synthesis , Synthesis
CCSSM
7.G.A.1, 7.G.A.2, 7.G.B.6, 7.RP.A.2, 7.RP.A.2.A, 7.RP.A.2.B 7.RP.A.3
NWDYK
How can you use scale factors to draw similar figures (scale drawings)?
How can you use scale factors to find missing information about angles measures? Side lengths? Area? Perimeter?
Emerging Mathematical Ideas
Continue to explore enlarging and shrinking rectangles and triangles and exploring how the scale factor impacts side lengths, perimeter, and area of new scale drawings but not the measures of the angles
- corresponding side lengths and perimeter of the similar figure increases or decreases by the scale factor (multiplier).
- area of similar figures increases or decreases by the scale factor squared (multiplier squared)
Expand understanding of how attributes of two similar figures are affected by the scale factor
- use the understanding to find lengths of corresponding side lengths that have missing measures
- use the understanding to find angle measures of corresponding angles that have missing measures.
3.3 Out of Reach: Finding Lengths with Similar Triangles
Arc of Learning
Synthesis, Synthesis
CCSSM
7.G.A.1, 7.G.A.2, 7.G.B.6, 7.RP.A.2, 7.RP.A.2.A, 7.RP.A.2.B, 7.RP.A.3
NWDYK
How can you use similar triangles to find a distance that is difficult to measure?
Emerging Mathematical Ideas
Introduce the term “nested triangles” and broaden understanding of similar triangles.
Use knowledge of similar figures/scale drawings and apply it to nested triangles to solve real world distance problems that are difficult to physically measure.
Mathematical Reflections
Arc of Learning
Synthesis, Synthesis
CCSSM
Responses to the reflection are informed by the work in the Investigation and thus also reflect: 7.G.A.1, 7.G.A.2, 7.G.B.6, 7.RP.A.2, 7.RP.A.2.A, 7.RP.A.2.B , 7.RP.A.3
Mathematical Reflection
What do you now know about similar figures? What do you know about proportional reasoning?
Emerging Mathematical Ideas
Continue exploration of proportional relationships between corresponding side lengths and perimeters of similar figures.
With similar figures, understand which attributes change and which stay the same:
- corresponding angles of two similar figures are the same measure while angles of non-similar figures may not be.
- corresponding side lengths and perimeter of the similar figure increases or decreases by the scale factor (multiplier).
- area of similar figures increases or decreases by the scale factor squared (multiplier squared)
Investigation 4: Similarity Figures and Ratios
Students will be working to develop elements of the following Unit Goals throughout Investigation 4.
Similar Figures (Scale Drawings): Understand what it means for figures to be similar
- Identify similar figures by comparing corresponding sides and angles
- Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures
- Recognize the role multiplication (ratios), plays in similarity relationships
- Recognize the relationship between scale factor and ratio in similar figures (scale drawings)
- Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings)
Proportional Reasoning: Develop proportional reasoning strategies in the context of similar figures
- Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas
- Contrast proportionality in the context of geometry (similarity) with numerical situations
- Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities
- Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures
- Use similarity (scaling) to solve real-world problems
4.1 Equivalent Ratios Within Similar Figures
Arc of Learning
Analysis & Analysis
CCSSM
7.RP.A.2, 7.RP.A.2.A 7.RP.A.2.B, 7.RP.A.3
NWDYK
What information do the ratios of adjacent side lengths within two similar figures provide about similar figures? How are these ratios helpful in solving problems?
Emerging Mathematical Ideas
Introduce the idea that ratios can be represented as fractions, extending their use from just comparison statements.
Explore the relationship between ratios of corresponding adjacent side lengths within two similar figures. Build off understanding of scale factor between similar figures to begin to understand why these ratios are equal.
4.2 Using Shadows to Find Heights
Arc of Learning
Synthesis, Synthesis
CCSSM
7.G.A.1, 7.RP.A.2, 7.RP.A.2.A, 7.RP.A.2.B, 7.EE.B.3, 7.EE.B.4
NWDYK
If two figures are similar, how can you use information about the figures to find unknown lengths, perimeters, areas, or angle measures?
Emerging Mathematical Ideas
Explore the use of similarity to solve real-world problems. Use understanding of similar figures, including scale factors and ratios, to find a distance that is difficult to measure.
Understand that ratios of corresponding adjacent side lengths within two similar figures are equal
- use scale factor and/or ratio relationships between corresponding side lengths to determine if two figures are similar
- use understanding of scale factor and/or ratios of adjacent sides to find missing lengths, perimeter, and area
4.3 More Imposters
Arc of Learning
Synthesis, Synthesis
CCSSM
7.G.A.1, 7.RP.A.1, 7.RP.A.2, 7.RP.A.2.A, 7.RP.A.2.B, 7.RP.A.3 , 7.EE.B.3
NWDYK
What are strategies for identifying if shapes have been scaled (similar figures) or if the shapes are imposters?
Emerging Mathematical Ideas
Continue using proportional relationships to determine scaled figures.
Compare and measure geometric figures that are both similar and non-similar figures
Mathematical Reflection
Arc of Learning
Synthesis, Synthesis
CCSSM
Responses to the reflection are informed by the work in the Investigation and thus also reflect: 7.G.A.1, 7.RP.A.2, 7.RP.A.2.A, 7.RP.A.2.B , 7.RP.A.3 , 7.EE.B.3, 7.EE.B.4
Mathematical Reflection
What do you now know about similar figures? What do you know about proportional reasoning?
Emerging Mathematical Ideas
Continue exploration of proportional relationships between corresponding side length and perimeter of similar figures.
With similar figures, understand and be able to articulate which attributes change and which stay the same:
- corresponding angles of two similar figures are the same measure while angles of non-similar figures may not be.
- corresponding side lengths and perimeter of the similar figure increases or decreases by the scale factor (multiplier).
- area of similar figures increases or decreases by the scale factor squared (multiplier squared)
- ratios of corresponding adjacent side lengths within two similar figures are equal
Assessments
Check-Up #1
| Question | CCSS(s) | Unit Goal(s) | Problem(s) |
|---|---|---|---|
| 1a | 7.G.A.1 7.RP.A.2.A 7.RP.A.2.B |
Recognize the role multiplication (ratios), plays in similarity relationships Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use similarity (scaling) to solve real-world problems |
1.1 1.2 1.3 |
| 1b | 7.G.A.1 7.RP.A.2.A |
Recognize the role multiplication (ratios), plays in similarity relationships Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use similarity (scaling) to solve real-world problems |
1.1 1.2 1.3 |
| 1c | 7.G.A.1 7.RP.A.2.A |
Recognize the role multiplication (ratios), plays in similarity relationships Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use similarity (scaling) to solve real-world problems |
1.1 1.2 1.3 |
| 1d | 7.G.A.1 7.RP.A.2.A 7.RP.A.2.B |
Recognize the role multiplication (ratios), plays in similarity relationships Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use similarity (scaling) to solve real-world problems |
1.3 |
Partner Quiz
| Question | CCSS(s) | Unit Goal(s) | Problem(s) |
|---|---|---|---|
| 1a | 7.G.A.1 7.RP.A.2 7.EE.B.4.A 7.NS.A.2 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.1 |
| 1b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.1 2.3 |
| 1c |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Contrast proportionality in the context of geometry (similarity) with numerical situations |
2.1 2.3 |
| 1d | 7.EE.B.4.A |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Contrast proportionality in the context of geometry (similarity) with numerical situations |
2.1 2.3 |
| 1e |
7.G.A.1 |
Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.2 |
| 1f |
7.G.A.1 |
Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.1 |
| 1g |
7.G.A.1 |
Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.1 |
| 1h |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas |
2.1 2.3 |
| 2a |
7.G.A.1 |
Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Contrast proportionality in the context of geometry (similarity) with numerical situations |
2.3 |
| 2b |
7.G.A.1 |
Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) |
2.3 |
| 2c |
7.G.A.1 |
Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Contrast proportionality in the context of geometry (similarity) with numerical situations |
2.3 |
Checkup #2
| Question | CCSS(s) | Unit Goal(s) | Problem(s) |
|---|---|---|---|
| 1a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.3 |
| 1b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.3 3.2 |
| 2a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
3.3 |
| 2b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
3.3 |
| 2c |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
3.1 |
| 2d |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
3.1 |
| 3a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) |
3.2 |
| 3b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) |
3.2 |
Unit Test
| Question | CCSS(s) | Unit Goal(s) | Problem(s) |
|---|---|---|---|
| 1a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles |
2.3 3.2 4.1 |
| 1b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
2.3 3.1 3.2 |
| 1c |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.3 3.2 4.1 |
| 1d |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
2.3 3.1 3.2 |
| 2a |
7.G.A.1 |
Recognize the role multiplication (ratios), plays in similarity relationships Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.1 2.2 4.3 |
| 2b |
7.G.A.1 |
Recognize the role multiplication (ratios), plays in similarity relationships Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
2.1 2.2 4.3 |
| 3a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) |
1.1 1.2 1.3 2.3 4.1 4.3 |
| 3b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Use informal methods, scale factors, and geometric tools, including algebraic rules that produce figures on a coordinate grid, to construct similar figures (scale drawings) Predict the ways that stretching or shrinking a figure will affect side lengths, angle measures, perimeters, and areas Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities Use similarity (scaling) to solve real-world problems |
1.1 1.2 1.3 2.3 4.1 4.3 |
| 4a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
1.1 1.2 2.3 4.1 |
| 4b | 7.RP.A.2.A |
Recognize the role multiplication (ratios), plays in similarity relationships Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
4.1 |
| 4c | 7.RP.A.2.A 7.G.A.1 7.RP.A.2 7.RP.A.2.A 7.RP.A.3 7.NS.A.2 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures |
4.1 |
| 5 |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities Informally solve proportions using scale factor or ratios to find missing side lengths on scaled (similar) figures Use similarity (scaling) to solve real-world problems |
4.2 |
| 6a |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 2.3 4.1 |
| 6b |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 2.3 4.1 |
| 6c |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 2.3 4.1 |
| 7 |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 1.3 2.1 2.2 2.3 3.1 3.2 3.3 4.1 4.2 4.3 |
| 8 Isaiah |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 2.3 4.1 |
| 8 Noah | 7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 2.3 4.1 |
| 8 Anna |
7.G.A.1 |
Identify similar figures by comparing corresponding sides and angles Use scale factors and ratios to describe relationships between corresponding side lengths, perimeters, and areas in similar figures Recognize the role multiplication (ratios), plays in similarity relationships Recognize the relationship between scale factor and ratio in similar figures (scale drawings) Stretch and shrink shapes to see that equivalent ratios are a multiplicative relationship between two quantities |
1.1 1.2 2.3 4.1 |
General Arc of Learning
Unit Arc of Learning
Knowledge of similarity is important to the development of students’ understanding of the geometry in their environment. In their immediate environment and in their studies of natural and social sciences, students frequently encounter phenomena that require familiarity with the ideas of proportional reasoning applied to the study of enlargement, scale factors, area growth, indirect measurement, and other similarity-related concepts. Similar figures are another name for scale drawings. A scale drawing is usually an enlarged, shrunk, or a replica of the original figure. In this Unit, for convenience, the original figure and its image are similar figures. This Unit uses the two terms interchangeably.
Using the context of number, the 6th grade Comparing Quantities Unit, provided an introduction to the basic concept of ratio, including equivalent ratios, unit rates, and rate tables. It included strategies for solving problems such as using tables, graphs, equivalent ratios, tape diagrams, and numeric reasoning.
To be fully developed, proportional reasoning needs to be revisited in various contexts. In this Unit, the geometric concept of similarity is used to strengthen students’ understanding of proportion.
Similarity will be revisited in 8th grade when the effects of transformations on geometric figures are studied, including which transformations maintain similarity. Proportional reasoning continues throughout 7th grade using different mathematical contexts in the Units Comparing and Scaling, How Likely Is It?, Filling and Wrapping, Moving Straight Ahead, and Samples and Populations.
Mathematical Overview
Mathematics Overview: Stretching and Shrinking
Key ideas: scale drawing, similar figure, scale factor, corresponding angles, corresponding sides, congruent triangles.
Major Focus: Proportional Reasoning, Geometry (this will link when available)
Strategic Connections: Variables, Equation, Coordinates (this will link when available)
In Stretching and Shrinking students use multiplicative reasoning and ratios to create and analyze scale drawings. These scale drawings are similar to the original. CMP always aims to provide opportunities for students to make connections and build meaning. Stretching and Shrinking connects back to Comparing Quantities in 6th grade and forward to the 8th Grade Unit Flip, Spin, Slide, and Stretch, where similarity and congruence are defined.
This Unit is the first step in making sense of similarity of geometric shapes. IN Shapes and Designs students drew congruent figures. They found that some combinations of conditions produce unique triangles. Congruent triangles are similar to each other, with a scale factor of 1, that is, they are identical. Students draw similar figures in this Unit, develop a working definition of similarity and scale factor, and use this to solve problems.
In roughly this order, students
- Use tools to construct similar figures.
- Use ratios to analyze and define similarity.
- Solve geometric problems about lengths and areas of similar figures.
- Use coordinate rules to draw similar figures.
- Develop an understanding of scale factor.
- Extend understanding of scale factor to encompass areas and perimeters of similar figures.
- Design similar figures and use proportional reasoning to find missing measures.
- Apply proportional reasoning to ratios within similar figures.
SCALE drawings, similarity
Scale Drawing Tools
rubber band stretcher
Students start with a home made version of a pantograph.
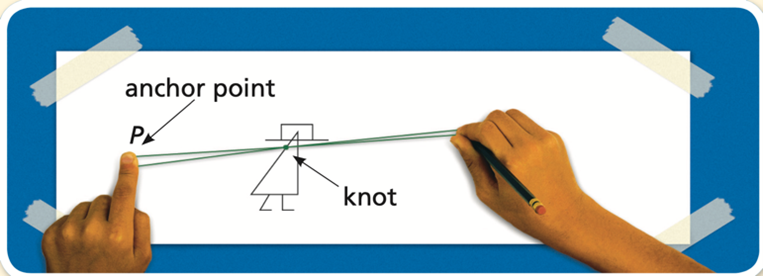
The reason this tool creates scale drawings is because it is actually creating embedded similar triangles. On the graphic above as the knot traces the highlighted line on the figure the pencil traces its image. In essence each original line and its image are corresponding sides of two similar triangles.
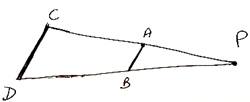
Of course we do not see the embedded triangles, PAB and PCD, when we use the rubber band stretcher, just the original figure and image.
.png)
You can alter the tool to make any whole number ratio. For example, the diagram shows how to make a scale drawing where image: original = 4:3.
Understanding ratios is crucial to understanding similarity or scale drawing. The ratios of corresponding lengths must be constant, and the sizes of the angles must be preserved.
Copier
A copier is a more accurate tool for making a proportional image. Any setting over 100% makes an enlargement. Any setting under 100% makes an image smaller than the original. For example, lengths on the Copy 2: lengths on the original = 150:100; lengths on the Copy 1: lengths on the original = 75:100 or 3:4.
.png)
Link to the Future: Students will solve percent problems about % increase and decrease later in 7th grade. In the copier examples Copy 2 is a 50% increase, and Copy 1 is a 25% decrease.
Scale Drawing Tools
Coordinates
Using coordinate rules emphasizes the multiplicative nature of the relationship between original and similar image. By exploring rules that solely multiply coordinate values, or solely add, students see that each of these transformations has a particular effect. For example, in the diagram below, focusing on length and location of ED under the impact of two different rules, we see image 1 of ED is the same size as the original but displaced or translated 2 units right and 3 up. But, image 2 of ED is half the size and half the distance from the origin. If we apply these rules to all the points the first rule will give a congruent figure; the second will give a similar figure with lengths all ½ the original and corresponding angles the same size. This echoes the rubber band experiment. The origin is the fixed point. (Distance to origin is also halved.)
.png)
| Original | Image 1 | Image 2 | |
|---|---|---|---|
| Rule | (x,y) | (x + 2, y + 3) | (0.5x, 0.5y) |
| Point E | (4, 3) | (6, 6) | (2, 1.5) |
| Point D | (6, 3) | (8, 6) | (3, 1.5) |
| Length ED | 2 | 2 | 1 |
Link to the Future: In 8th grade students study transformations. Transforming x, y by multiplying by a>1, (x,y) -> (ax, ay), creates a similar figure, an enlargement or dilation, with scale factor a. Transforming by multiplying by a < 1 creates a similar figure smaller than the original. Transforming by adding only, creates a congruent figure at a different location, a translation. Transforming by multiplying by a negative scale factor creates a double reflection.
Scale Factor: Impact on Lengths and Areas, Finding Missing Parts
Reptiles
Scale Factor
If lengths on an original figure are all multiplied by a, and all angles are preserved, then a similar figure will be obtained and the scale factor is a.
For figures on a coordinate grid, when an original figure is changed under the rule
(x, y) -> (ax, ay) the image will be similar and original length: image lengths = 1:a. The scale factor is a.
Impact on Area and Perimeter
Because perimeter is a one-dimensional measure, the scale factor has the same impact on perimeter as on length. For example, in the figure below, the scale factor relating lengths is 3. The perimeter of the original rectangle is 10cm and the perimeter of the image is 30cm. Original perimeter: Image perimeter = 10:30 or 1:3.
.png)
Area, however, is a two-dimensional measure. In this case, Original area to Image area = 6 sq. cm to 54 sq. cm. = 1:9. This is not the same ratio as corresponding lengths.
Exploring Rep-tiles
Using rep-tiles to create similar figures makes it clear how the scale factor connecting lengths relates to the ratio of areas. For example,
using 4 triangles .png) creates a similar figure with scale factor 2, using 9 triangles
creates a similar figure with scale factor 2, using 9 triangles.png) creates a similar figure with scale factor 3, using 16 triangles
creates a similar figure with scale factor 3, using 16 triangles .png) creates a similar figure with scale factor 4, etc.
creates a similar figure with scale factor 4, etc.
If the scale factor relating lengths is 1:a then the ratio of areas is 1:a2.
Students will discuss this as the change in area is
scale factor • scale factor or (scale factor)2.
Missing Parts
Missing Lengths
Because the ratio of corresponding lengths is consistent for similar figures, we can use the scale factor to find missing lengths.
In the example below the ratio of corresponding lengths is 3:5 or 1:5/3. It is important to pay attention to relative position in the figures. The shortest side in the original is 3cm; it corresponds to the shortest side in the image, 5 cm.
.png)
The scale factor is 5/3 or 1 2/3. This should remind students of work they did with equivalent ratios in 6th grade.
|
0riginal |
3 |
6 |
9 |
1 |
10 |
|---|---|---|---|---|---|
|
Image |
5 |
10 |
15 |
5/3 |
d |
To find the length labeled d in the image, we note that it corresponds to the length labeled 10cm in the original. Using the scale factor 5/3, d = 5/3 (10), or 16 2/3.
3 to 5, 1 to 5/3, and 10 to 16 2/3 are equivalent ratios.
Missing Angles
Because corresponding angles are equal for similar figures, we can find missing angles. In the above example, we have two angle measures given in the original triangle, 90 and 17. We know corresponding angles in the image are also 90 and 17. It is important to pay attention to the relative positions in the figures. The 90-degree angle should be opposite the longest side in each triangle. The 17-degree angle should be opposite the shortest side in each triangle. (Since we also know from Shapes and Designs that the angle sum of a triangle is 180 degrees, we can deduce 17 + 90 + x = 180. So, the remaining angle in both triangles is 73 degrees.)
Learning Aid
- 1.1 Photograph of Mystery Teacher
- 1.2 Super Sleuth
- 1.3 Super Sleuth Figure and Two Copies
- 2.1A Table of Coordinates Wumps Characters
- 2.1B Six First Quadrant Grids
- 2.1B Two Larger First Quadrant Grids
- 2.1B One Larger First Quadrant Grid
- 2.2A Table for Mug Hats
- 2.2B Six First Quadrant Grids
- 2.3 Wump Mouths and Noses
- 3.1A Quadrilaterals for Rep-Tiles
- 3.1B Triangles for Rep-Tiles
- 3.1C Rep-Tile Recording Sheet
- 3.2A Designing Under Constraint Figures
- 3.2B Polygon Sets
- 3.3 River Diagrams
- 4.1A Initial Challenge Sets 1-3
- 4.1B What If, Situation A: Sets 4-7
- 4.1C Ratio Recording Sheet
- 4.2 Diagrams
- 4.3 Similar or Imposter Sets
Teaching Aids
- 2.1A 4 by 4 Game Grid
- 2.1B Table of Coordinates Answers
- 2.1C Wump Characters No Grid
- 2.1D Wump Characters on Grid
- 2.2 Wump Hats on Grids
- 3.1A Answers for Quadrilateral Rep-Tiles
- 3.1B Answers for Triangles Rep-Tiles
- 4.1 Using Proportions to Find Scale Drawings
- 4.2 Sample Missing Triangle Length
- 4.3 Sets with Measures
Family Letter
View Family Letter.
Assessments
Applications-Connections-Extensions (ACE) Homework
© 2021 Connected Mathematics Project at Michigan State University
Do not copy, share, or duplicate without permission.